Простейшие = решаемые аналитически обыкновенные дифференциальные уравнения первого порядка. Виды дифференциальных уравнений первого порядка.

Простейшие = решаемые аналитически обыкновенные дифференциальные уравнения первого порядка. Виды дифференциальных уравнений первого порядка.

Уравнения с разделяющимися переменными и сводящиеся к ним
Однородные уравнения и сводящиеся к ним
Линейные уравнения и сводящиеся к ним
Уравнение в полных дифференциалах . Интегрирующий множитель.
Уравнения не разрешенные относительно производной и сводящиеся к ним

Уравнения с разделяющимися переменными и сводящиеся к ним

1. y'=f(x)*g(y) - например: y'=x*y*(y+2), где f(x)=х; g(y)=y*(y+2)

или

m(x)*n(y)dy+p(x)*q(y)dx=0

(Примеры и методы решений)

2. Уравнение вида y'=f(ax+by) приводится к уравнению с разделяющимися переменными

(Примеры и методы решений)

Однородные уравнения

1. y'=f(y/x)

или

M(x,y)dx+N(x,y)dy=0,

где M(x,y) и N(x,y) однородные функции одной и той же степени "n".

(Примеры и методы решений)

2. 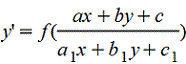сводится к однородному уравнению.

(Примеры и методы решений)

Линейные уравнения

1. y'+a(x)y=b(x)

(Примеры и методы решений)

2. Уравнение y'+a(x)y=b(x)yⁿ (Бернулли) сводится к однородному

(Примеры и методы решений)

3. Уравнение y'+a(x)y+b(x)y²=c(x) (Риккати) в некоторых случаях сводится к уравнению Бернулли.

(Примеры и методы решений)

Уравнение в полных дифференциалах. Интегрирующий множитель.

1. M(x,y)dx+N(x,y)dy=0,

если выполняется условие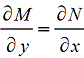

Интегрирующий множитель- множитель, умножив на который обе стороны уравнения, мы получим уравнение в полных дифференциалах (если оно таким и не было изначально).

Уравнения не разрешенные относительно производной

Общий вид : F(x,y,y')=0,

1. Случай, когда из уравнения F(x,y,y')=0 можно выразить y' через x, y.

2. Случай, когда уравнение F(x,y,y')=0 можно разрешить относительно у (простейший вариант метода введения параметра).

3. Случай, когда уравнение F(x,y,y')=0 можно разрешить относительно х.

4. Уравнение Лагранжа y=xφ(y')+ψ(y'). Уравнение Клеро y=xy'+ψ(y')

5. Особые решения.