Введение в дифференциальные уравнения.
- Понятие математической модели физического процесса и пример. Определение дифференциального уравнения.
- Определение обыкновенного дифференциального уравнения.
- Определение обыкновенного дифференциального уравнения порядка 'n'.
- Определение решения дифференциального уравнения.
- Определение решения дифференциального уравнения.Определение общего интеграла (неразрешенного относительно у решения)
- Задача Коши. Граничные условия.
- Определение порядка дифференциального уравнения.
- Определение уравнения с частными производными.
Метод исследования физических процессов является математическим по своему существу.
1) Определение (понятие) дифференциального уравнения. При рассмотрении многих физических явлений вводят функции, описывающие этот процесс. Бывает трудно найти закон связывающий введенные величины. Но часто проще бывает установить связь между функцией, ее производными и независимыми переменными (дифференциальные уравнения). Эта зависимость называется математической моделью данного физического процесса и одновременно является дифференциальным уравнением.
Пример.
Тело, имеющее в момент времени t=0, температуру To , помещается в среду, температура которой T1 (To >T1 ). Как изменяется температура тела в зависимости от времени?
Искомую функцию - температуру обозначаем u(t). Известно, что скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. Ясно, что u(t) убывающая функция. В силу механического смысла производной имеем 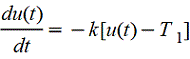 , k - коэффициент пропорциональности. , k - коэффициент пропорциональности.
Полученное соотношение (дифференциальное уравнение) и есть математическая модель данного процесса (физического явления).
2) Определение (понятие) обыкновенного дифференциального уравнения. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным.
3) Определение (понятие) обыкновенное дифференциальное уравнение порядка "n" имеет следующий вид:
F(x,y,y',y'',..,y(n))=0
Следовательно, диффернциальное уравнение первого порядка имеет вид
F(x,y,y')=0
Здесь F известная функция от "n+2" переменных, удовлетворяющая определенным условиям непрерывности, дифференцируемости, а y=y(x) - функция, которую надо найти.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
4) Определение (понятие) решения (не общего) дифференциального уравнения на интервале (a,b) называется функция, имеющая на этом интервале производные y,y',y'',..,y(n) и удовлетворяющая для всех х∈ (a,b) уравнению.
График решения обыкновенного дифференциального уравнения называется интегральной кривой этого уравнения.
5)Определение (понятие) общего решения дифференциального уравнения
Общее решение содержит все решения уравнения. Общее решение уравнения n-го порядка содержит "n" произвольных постоянных и имеет вид y=φ(x, c1, c2,..,cn)
Если соотношение, связывающее x, y и "n" произвольных постоянных, дано в виде, не разрешенном относительно y:
φ(x,y,c1, c2,..,cn )=0, (квазиобщее решение) это будем называть такое соотношение общим интегралом уравнения.
Процесс нахождения решений уравнения называется интегрированием дифференциального уравнения.
6) Задача Коши. Понятие (определение) граничных условий.
Задача Коши состоит в отыскании решения уравнения F(x,y,y',y'',..,y(n))=0, удовлетворяющего условиям при x=xo , y(xo)=yo ...... y(n-1)(xo)=y(n-1)o - граничные (начальные условия задачи Коши), где xo ,yo , y1o, y2o,...,y(n-1)o, - заданные числа. Другими словами задача Коши состоит в нахождении такого решения, которое удовлетворяет начальным условиям. Любая реальная задача - задача Коши. Решение уравнения в общем виде не является решением задачи Коши.
7) Определение (понятие) уравнения с частными производными. Если искомая функция "z" зависит от нескольких независимых переменных x1 ,х2 ,.., хn (n≥2), то уравнение называется уравнением с частными производными. При n=2, уравнение имеет вид:
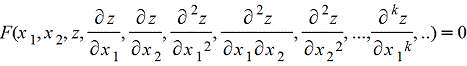 , ,
здесь F - заданная функция
z(x1,x2) - искомая функция.
|
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Основные определения раздела дифференциальные уравнения.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Основные определения раздела дифференциальные уравнения.
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Основные определения раздела дифференциальные уравнения.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Основные определения раздела дифференциальные уравнения.
