Линейные однородные дифференциальные уравнения 2-го порядка с переменными коэффициентами.
Рассматривается уравнение
ao(x)y''+a1(x)y'+a2(x)y=0, где (ao(x), a1(x), a2(x)) - непрерывные функции на некотором интервале (a,b).
Предположим, что известночастное решение y1(x)этого уравнения. Чтобы получить общее решение y(x), рекомендуется воспользоваться формулой Острогадского - Лиувилля
,
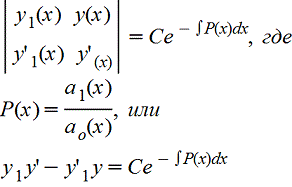а это уже уравнение 1го порядка относительно y(x). Далее, деля левую и правую части на y12(x) , имеем
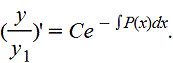
После интегрирования получим общее решение исходного уравнения.
Замечание 1.
Общего способа отыскания частного решения y1(x) линейного уравнения не существует. Иногда удается найти его путем подбора или в виде алгебраического многочлена y1(x)=xn+a1xn-1+...+an или в виде показательной функцииy1(x)=eax или и т.д.
Замечание 2.
Если известно y1(x), то порядок уравнения можно понизить, сохраняя линейность и следующим способом. В исходное уравнение надо подставить y1(x)z(x) и затем сделать замену z'(x)=u(x). Но лучше все же пользоваться формулой Острогадского - Лиувилля.
(
Примеры и методы решений)
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Линейные однородные дифференциальные уравнения 2-го порядка с переменными коэффициентами.