Примеры решений линейных однородных дифференциальных уравнений 2-го порядка с переменными коэффициентами.
Пример 1.
Найти общее решение уравнения
(2x+1)y''+(4x-2)y'-8y=0, x≠-1/2
Попробуем найти частное решение в виде y1(x)=eax.
Найдем "а". Для этого y1(x)=eax подставим в уравнение.
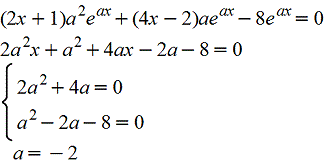
Итак, y1(x)=e-2x является частным решением.
Для того чтобы найти лбщее решение, воспользуемся формулой Острогадского - Лиувилля
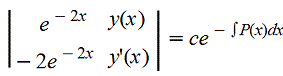
Здесь p(x)=(4x-2)/(2x+1)
Вычислим интегал
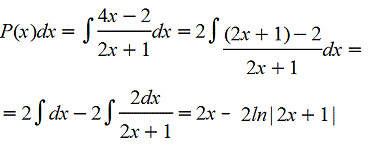
Итак,
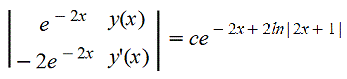
или
e-2xy'+2-2xy=Ce-2x(2x+1)2
Делим на y12(x),
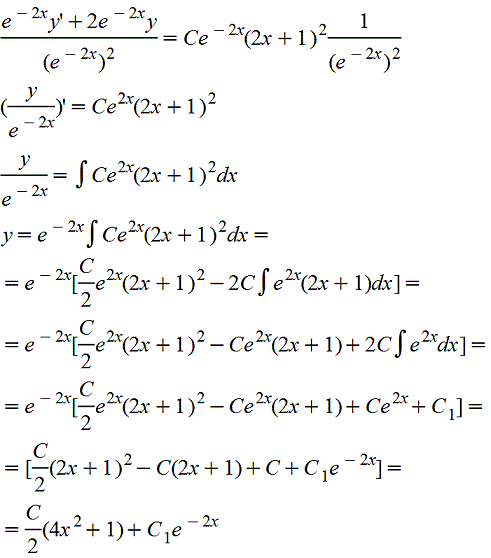
При вычислении интеграла 2 раза воспользовались формулой интегрирования по частям
y(x)=(C/2)(4x2+1)+C1e-2x - общее решение исходного уравнения.
Пример 2.
Найти общее решение уравнения
(1-x2)y''-2xy'+2y=0 на (1;1).
Попробуем найти частное решение y1(x) в виде алгебраического многочлена. Для этого подставим y1(x)=xn+a1xn-1+...+an
Выписываем только члены с самой старшей степенью "х". Приравнивая к нулю коэффициент при старшей степени "х", определим степень многочлен
-n(n-1)+2n+2=0,
n2-3n+2=0 n=1; n=2
частным решением будет и y1=x+a и y1=x2+ax+b
Возьмем за y1(x)=x+a. Чтобы найти "a", опять подставим y1=x+a в исходное уравнение
-2x+2x+2a=0
a=0
Итак, y1=x является частным решением.
Для нахождения общего решения воспользуемся формулой Острогадского - Лиувилля
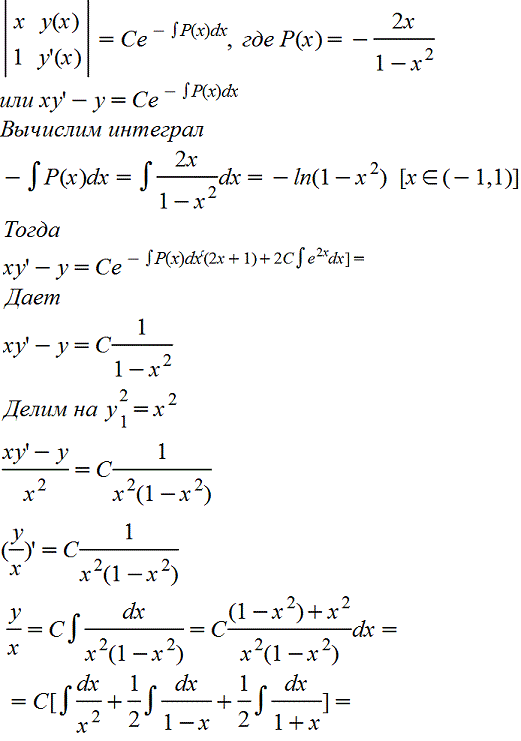
(Интеграл разбили на два
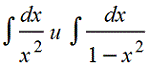
и во втором интеграле воспользовались тем, что
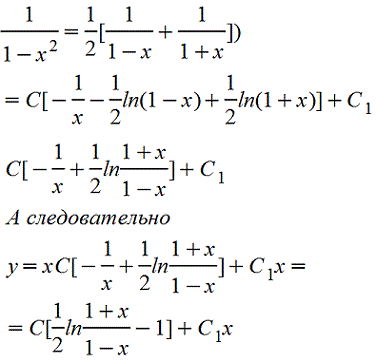
Пример 3
Найти общее решение уравнения
x2y''-xy'-3y=0 x>0 если известно что
y1(x)=1/x - частное решение
Проверим, что y1(x)=1/x - частное решение. Для этого подставим y1(x)=1/x в уравнение y1'(x)=-1/x2 , y''=2/x3
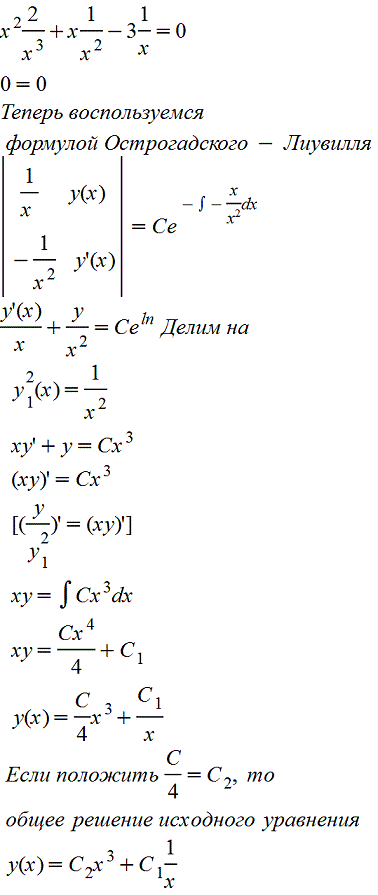
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Линейные однородные дифференциальные уравнения 2-го порядка с переменными коэффициентами. / / Примеры решений линейных однородных дифференциальных уравнений 2-го порядка с переменными коэффициентами.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Линейные однородные дифференциальные уравнения 2-го порядка с переменными коэффициентами. / / Примеры решений линейных однородных дифференциальных уравнений 2-го порядка с переменными коэффициентами.
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Линейные однородные дифференциальные уравнения 2-го порядка с переменными коэффициентами. / / Примеры решений линейных однородных дифференциальных уравнений 2-го порядка с переменными коэффициентами.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Линейные однородные дифференциальные уравнения 2-го порядка с переменными коэффициентами. / / Примеры решений линейных однородных дифференциальных уравнений 2-го порядка с переменными коэффициентами.
