Дифференциальные уравнения, не разрешенные относительно производной.

Дифференциальные уравнения, не разрешенные относительно производной.

F(x,y,y')=0

1. Из уравнения F(x,y,y')=0 выразить y' через x и y. Получится одно или несколько уравнений вида y'=f(x,y), каждое из которых надо решить.

Пример.

у'²-y²=0

y'=y и y'=-y

dy/y=dx и dy/y=-dx

ln|y|=x+lnC и ln|y|=-xlnD

y=Ce^x и y=De^-x

2. Метод параметра (простейший вариант метода).

Пусть уравнение F(x,y,y')=0 можно разрешить относительно y.

y=f(x,y').

Введем параметр p=y'=dy/dx

Тогда y=f(x,p)

Возьмем полный дифференциал от обеих частей, заменив dy через pdx, получим

pdx=f_x'dx+f_y'dy

Если решение этого уравнения найдено в виде x=φ(p), то получим решение исходного уравнения в параметрической форме: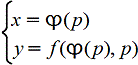

Пример

y=ln(1+y'²)

p=y'=dy/dx, y=ln(1+p²)

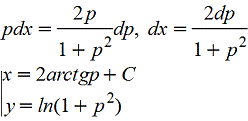
При делении на р потеряли решение у=0

3. Если уравнение F(x,y,y')=0 можно разрешить относительно х:

x=f(y,y'), то также как в 2 вводим параметр p=y'=dy/dx

4. Уравнение Лагранжа

y=xφy'+Ψ(y')

и уравнение Клеро

y=xy'+Ψ(y')

являются частными случаями, рассмотренными в пункте 2.

5) Немного об особых решениях. Решение y=φ(х) уравнения F(x,y,y')=0 называется особым, если через каждую его точку, кроме этого решения, проходит и другое ршение, имеющее в этой точке ту же касательную, что и решение φ(х), но не совпадающее сним в сколь угодно малой окрестности этой точки. Пусть F(x,y,y'), δF/δy и δF/δy' непрерывны. Тогда любое особое решение уравнения F(x,y,y')=0 удовлетворяет и уравнению δF(x,y,y')/δy'=0.

Чтобы отыскать особые решения, надо из системы

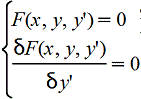исключить y'. Полученное уравнение называется дискриминантной кривой. Для каждой ветви дискриминантной кривой надо проверить, является ли эта ветвь решением и если является, то будет ли оно особым (т.е. нарушается ли единственность в каждой его точке).

Пример.

y=xy'-y² - Уравнение Клеро

p=y'=dy/dx, y=xp-p²

pdx=pdx+xdp-2pdp

(x-2p)dp=0

dp=0, p=c, следовательно

x=2p, y=xp-p²

y=Cx-C² или y=(x²/2)-(x²/4)

y=x²/4-особое решение

y=x²/4 решение исходного уравнения. Докажем, что особое.

Берем произвольную точку на решении y=x²/4, например (x_o,x²_o/4). найдем С, при котором прямая y=Cx-C² также проходила через эту точку x²_o/4=Cx_o-C², следовательно C=x_o/2, т.е. y=(x_o/2)x-(x²_o/4).