Примеры решений линейных дифференциальных уравнений (и сводящихся к ним)

Примеры решений линейных уравнений (и сводящихся к ним)

1. y'+a(x)y=b(x)

Сначала надо решить методом разделения переменных однородное уравнение y'+a(x)y=0. В общем решении однородного уравнения заменить произвольную постоянную "с" на неизвестную функцию с(х) и подставить в исходное уравнение.

Пример.

xy'-2y=2x⁴

y'-(2/x)y=2x³

y'-(2/x)y=0, dy/y=2dx/x

ln|y|=2ln|x|+lnc

y=cx²

y=(x)x²

c'x²+2cx-(2/x)*c)x²=2x³

(dc/dx)*x²=2x³

dc=2xdx

c(x)=x²+c₁

Тогда y=c(x)x²=(x²+c₁)x²=cx²+ x⁴

2. Уравнение y'+a(x)y=b(x)yⁿ называется уравнением Бернулли.

Чтобы решить это уравнение, надо обе его части разделить на yⁿ и сделать замену z=1/y^n-1. После замены получается линейное уравнение.

Пример.

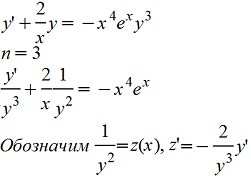
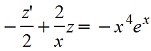линейное уравнение.

Решаем относительно z однородное

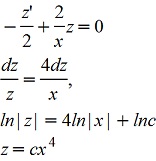
Подставляя z=c(x) в линейное, получим

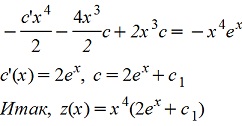
А решением исходного уравнения будет y≡0 (которое потеряли при делении на y³ исходного уравнения) и y^-2=x⁴(2e^x+c₁)

3) Уравнение y'+a(x)y+b(x)y²=c(x) (Риккати) в общем случае не решается в квадратурах.

Если же известно одно его частное решение y₁(x), то заменой y=y₁(x)+z(x) уравнение Риккати сводится к уравнению Бернулли. Иногда частное решение удается подобрать, исходя из вида свободного члена уравнения, т.е. члена, не содержащего у.

Пример

Для уравнения y'+y²=x²-2x в левой части будут члены, подобные членам правой части, если взять y=ax+b.

Подставим y=ax+b в уравнение и приравняем коэффициенты при подобных членах

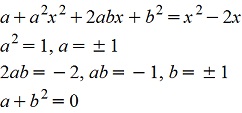
если a=+1, b=-1, то a+b²≠ 0

если a=-1, b=1, то a+b²=0

Итак, y=-x+1частное решение исходного уравнения.

Теперь делаем замену y=-x+1+z(x) и подставляем в исходное уравнение

-1+z'+x² +1+z²-2x-2xz+2z=x²-2x

z'+(2-2x)z=-z², получили уравнение Бернулли.