Примеры решение уравнений в полных дифференциалах

Примеры решений уравнение в полных дифференциалах. Интегрирующий множитель.

1. M(x,y)dx+N(x,y)dy=0, назывется уравнением в полных диференциалах, если его левая часть является дифференциалом некоторой функции u(x,y).

Тогда уравнение можно записать в виде 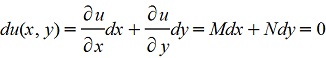и, следовательно, общее решение будет u(x,y)=c,

Условие 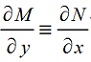является необходимым и достаточным условием того, чтобы уравнение было в полных дифференциалах.

Пример.

2xydx+(x²-y²)dy=0

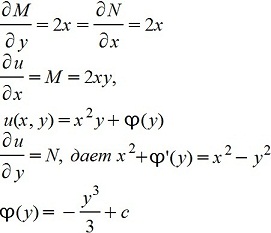
Можно взять u(x,y)=x²y-y³/3

А тогда общее решение x²y-(y³/3)+с

Если левая часть уравнения Mdx+Ndy=0 не есть полный дифференциал, то возникает задача нахождения такой функции µ(x,y), при умножении на которую левая часть уравнения становится полным дифференциалом. Функция µ(x,y) называется интегрирующим множителем

2. Интегрирующий множитель.

Нахождение интегрирующего множителя сводится к нахождению хотя бы одного частного решения уравнения в частных производных .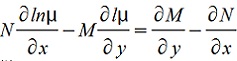

В общем случае интегрирование последнего уравнения является задачей не простой. Однако, считается, что интегрирующий множитель имеет заданный вид (например, является функцией только (х+у), или (x²+y²), или функцией только от (х), или только от (у) и т.д.) можно проинтегрировать 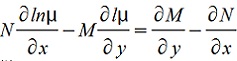и указать условия, при которых интегрирующий множитель заданного вида существует Тем самым выделяются классы уравнений, для которых интегрирующий множитель может быть найден.

Например, если 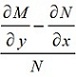является функцией только х, то интегрирующий множитель, зависящий лишь от х, существует и равен .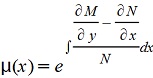

Замечание.

Можно доказать существование решения 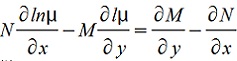в некоторой области, если функции M и N имеют непрерывные производные, и по крайней мере одна из этих функций не обращается в нуль. Следовательно, метод интегрирующего множителя можно рассматривать как общий метод интегрирования уравнений вида M(x,y)dx+N(x,y)dy=0.

Но ввиду трудности нахождения интегрирующего множителя этот метод применяется лишь в тех случаях, когда интегрирующий множитель очевиден.