Примеры решений однородных дифференциальных уравнений (и сводящихся к ним)
1. y'=f(y/x) или M(x,y)dx+N(x,y)dy=0, где M(x,y) и N(x,y) однородные функции одной и той же степени "n", т.е. М(kx,ky)≡ kn M(x,y);
N(kx,ky)≡ kn N(x,y)
Заменой y=tx получается уравнение с разделяющимися переменными.
Пример.
(x+2y)dx-xdy=0
y=tx, dy=tdx+xdt
(x+2tx)dx-x(tdx+xdt)=0
x(1+2t-t)dx=x2dt, x(1+t)dx=x2dt
Делим на x2(1+t), получаем dx/x=dt/(1+t),
ln|x|=ln|1+t|+lnc
x=c(1+t)
x=c(1+y/x) или х+у=сx2
При делении потеряли решение х=0 и у=-х, но последнее решение входит в х+у=сx2 при с=0.
2. 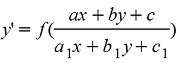 сводится к однородному при помощи переноса начала координат в точку пересечения прямых ax+by+c=0 и
a1x+b1y+c1=0.
Пример.
(2x-4y+6)dx+(xy+3)dy=0
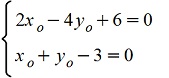
xo = 1, y o = 2
Сделаем замену 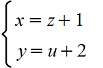 , здесь z-новая независимая переменная, u(z) - новая неизвестная функция.
(2z-4u)dz+(z+u)dy=0 получили однородное уравнение. Если же прямые ax+by+c=0 и a1x+b1y+c1=0 не пересекаются, то ax+by=k(a1x+b1y), и следовательно, уравнение имеет вид y'=F(ax+by), о котором говорилось в предыдущем пункте.
|
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений простейших = решаемых аналитически обыкновенных дифференциальных уравнений первого порядка. / / Примеры решений однородных дифференциальных уравнений (и сводящихся к ним)