Примеры решений дифференциальных уравнений с разделяющимися переменными (и сводящихся к ним)
1.Общий вид y'=f(x)*g(y), х∈ (a,b)
или
m(x)*n(y)dy+p(x)*q(y)dx=0, х∈ (a,b)
Для решения такого уравнения, надо обе части умножить или разделить на такое выражение чтобы в одну часть уравнения входил только х, в другую только y, а затем проинтегрировать обе части.
При этом при делении могут быть потряны решения.
Пример:
y'-xy2=2xy
y'=xy(y+2)
Делим на y(y+2)
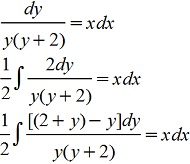
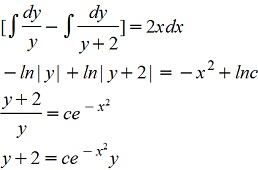
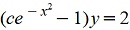
При делении на y(y+2) потеряно решение у=0
2) Уравнение вида y'=f(ax+by) приводятся к уравнениям с разделяющимися переменными заменой z=ax+by или z=ax+by+c где с любая
константа.
Пример.
y'=cos(y-x)
замена z(x)=y(x)-x
y'=z'+1
z'+1=cosz
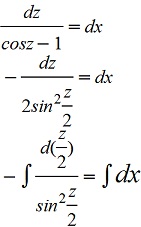
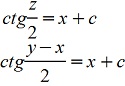
При делении на (cosz-1) потеряли решение cosz-1=0; z=2πk, k∈ z. y-x= 2πk
| 
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений простейших = решаемых аналитически обыкновенных дифференциальных уравнений первого порядка. / / Примеры решений дифференциальных уравнений с разделяющимися переменными (и сводящихся к ним)