Примеры решений дифференциальных уравнений, допускающих понижение порядка.
1.Пусть уравнение имеет вид F(x,y(k),..,y(n))=0, т.е. в уравнение не входит искомая функция. Тогда за новую неизвестную функцию берем низшую из производных, т.е. y(k)=z(x)
Пример 1:
x2y''=y'2
Обозначим
y'(x)=z(x), тогда x2z'=z2 , подставляем в исходное уравнение и переносим в левую часть все, что с "z", а в правую все с "x" (делим переменные).
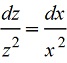 , интегрируем, получаем , интегрируем, получаем
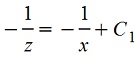 , или , или
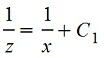 , приводим к общему знаменателю , приводим к общему знаменателю
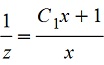 ;отсюда выражаем "z" ;отсюда выражаем "z"
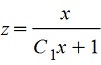 . Теперь возвращаемся к исходным обозначениям . Теперь возвращаемся к исходным обозначениям
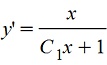 ; т.к. y'=dy/dx, то поделив обе части уравнения на dx получим ; т.к. y'=dy/dx, то поделив обе части уравнения на dx получим
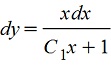 . Далее путем интегрирования ищем значение "у" . Далее путем интегрирования ищем значение "у"
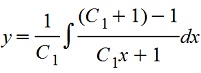
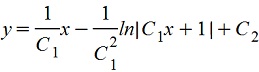
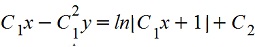
При делении потеряли решения z=0, y'=0, y=c, z=x, y'=x, y=x2/2+c
2) Путь в уравнение не входит x, т.е. уравнение имеет вид F(y,y',y'',...,y(n))=0.
Тогда порядок уравнения можно понизить, взяв за новую независимую переменную у, а за неизвестную функцию у'=p(y)
Пример 2.
y''=2yy'
Полагаем y'=P(y), тогда
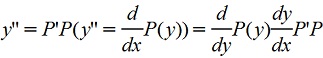 , следовательно , следовательно
P'P=2yP
P=0; P'=2y
y'=0; dp=2ydy
y=c; p=y2+C1 ; y'=y2+C1
a) при C1>0, т.е. C1=С2
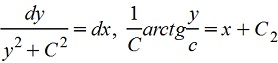
или y=Ctg(Cx)+C3
б) при C1<0, т.е. C1 =- C2
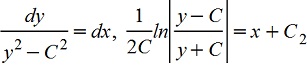
в) при C1=0
y'=y2, dy/y2=dx, -1/y=x+c
y=-1/(x+c)
3. Если уравнение однородно относительно "у" и его производных, т.е. не меняется от замены y, y', y'',...на ky, ky', ky'',... , то порядок можно понизить заменой: y'=yz, где z(x)- новая неизвестная функция.
Пример 3.
y(xy''+y')=xy'2(1-x)
Если подставить вместо y=ky, y'=ky', y''=ky'', то получим новое уравнение k2y(xy''+y') =k2xy'2 (1-x), которое отличается от исходного на множитель k2, который можно сократить.
Итак, делаем замену y'=yz и приводим исходное уравнение к виду y 2xz'+z2y2x+y2z =xy2z2(1-x)
или
y2x(z'+z+z2x2)=0
Откуда получаем решение у=0 и уравнение Бернулли xz'+z=-x2z2
Делим обе части на z2 и делаем замену 1/z=u, тогда уравнение приводится к линейному уравнению xu'-u=x2.
Заметим, что при делении на z2 потеряли решение z≡0, т.е. y'=0, т.е. у=с
Решая линейное уравнение получим u=x2+Cx
Тогда 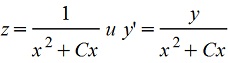
Имеем два случая: При С=0, y=C1e-1/x
При C≠ 0 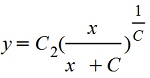
4) Если уравнение F(x,y,y',...,yn) =0 не отличается от уравнения F(kx, kmy,km-1y',km-ny(n) )=0 при некотором "m" (уравнение называется обобщенно однородным, то исходное уравнение сводится к уравнению, не содержащему "х" при помощи замены x=et, y=z(t)emt
Пример 4:
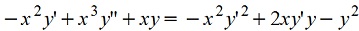 . .
Заменим x→ kx, y→ kmy, y'→ km-1y', y''→ km-2y'' , получаем km+1(-x2y'+x3y''+xy)=k2m(-x2y'2+2xy'y- y2)
Приравниваем степени k: m+1=2m⇒m-1 . Т.е. исходное уравнение при m=1 является обобщенно однородным.
Делаем замену x=et, y=z(t)et
т.к. y'x=y't/x't , то y'x=z'+z, y''xx=(z''+z')e-t
Подставляем y' и y'' в исходное уравнение, и после приведения подобных членов, получаем z''+z'2=0, т.е. уравнение, не содержащее искомую функцию.
|
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений обыкновенных дифференциальных уравнений порядка выше первого. / / Примеры решений дифференциальных уравнений, допускающих понижение порядка.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений обыкновенных дифференциальных уравнений порядка выше первого. / / Примеры решений дифференциальных уравнений, допускающих понижение порядка.
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений обыкновенных дифференциальных уравнений порядка выше первого. / / Примеры решений дифференциальных уравнений, допускающих понижение порядка.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений обыкновенных дифференциальных уравнений порядка выше первого. / / Примеры решений дифференциальных уравнений, допускающих понижение порядка.
