Примеры решений линейных однородных уравнений с постоянными коэффициентами.
aoy(n)(x)+a1y(n-1)(x)+...+an-1y'(x)+any(x)≡0, ao,a1,...,an-1,an - const.
Составляем характеристическое уравнение aoλn+a1λn-1+...+an-1λ+an=0.
Находим все его корни.
Общее решение исходного уравнения (yoo) есть сумма, состоящая из следующих слагаемых. Каждому простому вещественному корню λ отвечает слагаемое Ceλx. Каждому вещественному корню кратности "k" отвечает слагаемое (Co+C1x+C2x2+ Ck-1xk-1)eλx.
Каждой паре простых комплексно-сопряженных корней λ=α±βi отвечает слагаемое b1eαxcosβx+b2eαxsinβx. Каждой паре сопряженных корней λ=α±βi с кратностью "k" отвечает слагаемое (ao+a1x+...+ak-1xk-1)eαxcosβx+(do+d1x+...+dk-1xk-1 )eαxsinβx.
Пример 1:
y'''-8y=0, составляем характеристическое уравнение
λ3-8=0,
λ3- 23=0, по формуле сокращенного умножения получаем,
(λ-2)(λ2+2λ+4)=0, откуда корни уравнения
λ1=2
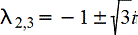
Возвращаемся к исходным обозначемниям, выражаем у
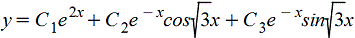
Пример 2:
y3+8y'''+16y'=0, составляем характеристическое уравнение
λ5+8λ3+16λ=0, выносим общий множитель за скобки
λ(λ4+8λ2+16)=0, сворачиваем то, что в скобках по формуле сокращенного умножения
λ(λ2+4)2=0, ищем корни
λ1=0
λ2,3=±2i (кратность k=2), возвращаемся к исходным обозначениям, выражаем у
y=C1+(C2+C3x)cos2x+(C4+C5x)sin2x
Пример 3:
y'''+2y''+y'=0, составляем характеристическое уравнение
λ3+2λ2+λ=0, выносим общий множитель за скобки
λ(λ2+2λ+1)=0, сворачиваем то, что в скобках по формуле окращенного умножения
λ(λ+1)2=0, ищем корни
λ1=0
λ2,3=-1 (кратность k=2), возвращаемся к исходным обозначениям, выражаем у.
y=C1+(C2+C3x)e-x
| 
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений обыкновенных дифференциальных уравнений порядка выше первого. / / Примеры решений линейных однородных уравнений с постоянными коэффициентами.