Примеры решений линейных неоднородных уравнений с постоянными коэффициентами.
Частное решение неоднородного (уч.н.) уравнения с постоянными коэффициентами.
aoy(n)(x)+a1y(n-1)(x)+...+any(x)=f(x).
Частное решение уравнения можно найти методом вариации постоянных, если известно общее решение соответствующего однородного уравнения yoo=C1y1(x)+C2y2(x)+...+Cnyn(x).
Считаем C1,C2,...,Cnзависящими от х, т.е.
y=C1(х)y1(x)+C2(х)y2(x)+...+Cn(х)yn(x).
C1(х),C2(х),...,Cn(х) находятся из системы:
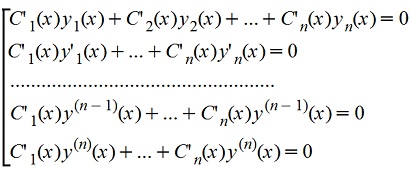
Если правая часть уравнения имеет вид f(x)=eαx[P(x)cosβx+Q(x)sinβx]), где P(x), Q(x) многочлены, то можно частное решение (yч.н.)искать в виде уч.н.=xseαx[R(x)cosβx+ T(x)sinβx].
Здесь или s=0, если число α+βi не является корнем характеристического уравнения или s равно кратности корня характеристического уравнения. А R(x) и T(x) многочлены степени, равной наибольшей из степеней многочленов R и Q. Чтобы найти коэффициенты многочленов R(x) и T(x), надо yч, y'ч , ..., y(n)ч подставитьв исходное уравнение и приравнять коэффициенты при подобных членах.
Если правая часть уравнения состоит из нескольких слагаемых вида aoy(n)(x)+a1y(n-1)(x)+...+any(x)=f(x), т.е. f(x)=f1(x)+f2(x)+...+fk(x), то частное решение уравнения с правой частью f(x) равно сумме частных решений уравнений с правыми частями f1(x),f2(x),...,fk(x).
Общее решение этого уравнения (yо.н.) равно сумме частного решения (уч.н.) и общего решения соответствующего однородного уравнения (yо.о.)
yо.н.=уч.н.+yо.о.
Пример 1:
y''-3y'+2y=e3x
λ2-3λ+2=0,
λ1=1,λ2=2
y=С1ex+С2e2x.
yч=С1(x)ex+С2(x)e2x
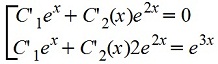
Из системы получаем
С'1(x)=-e2x
С'2(x)=ex
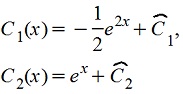
Для частного решения можно взять
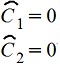
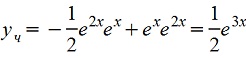
А общее решение
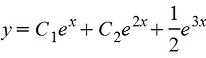
Пример 2:
y''+2y'-3y=x2ex
Правая часть имеет вид
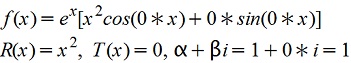
Характеристическое уравнение
λ2+2λ-3=0 имеет корни
λ1=1
λ2,3=-3
И следовательно, α+βi=1 является корнем характеристического уравнения кратностью 1. Поэтому частное решение ищем в виде
y=C1+(C2+C3x)cos2x+(C4+C5x)sin2x
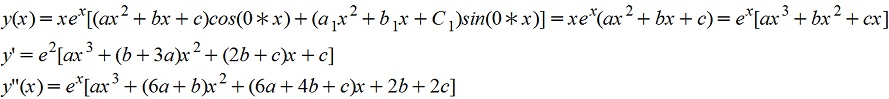
Подставляя yч, y'ч, y''ч, в исходное уравнение имеем
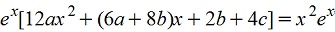 , сокращаем ех . Приравниваем коэффициенты при подобных членах , сокращаем ех . Приравниваем коэффициенты при подобных членах
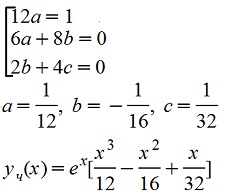
Общее решение соответствующего однородного уравнения (yоо) имеет вид
yоо=С1ех+С2е-3х
Общее решение неоднородного уравнения (yон)
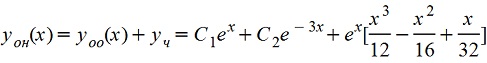
Пример 3:
y''+y=xsinx
Представим правую часть уравнения в виде
f(x)=eox[0*cosx+xsinx]
α=0, β=1, α+βi=i, P(x)=0, Q(x)=1
λ2+1=0, λ1,2=±i
α+βi является корнем характеристического уравнения кратности 1
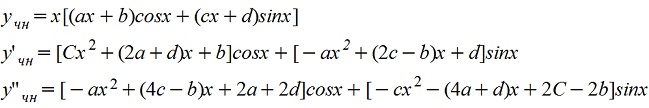
Подставляем в исходное уравнение у и приравниваем коэффициенты при подобных членах:
(4Cx+2a+2d)cosx+(-4ax+2c-2b)sinx=xsinx
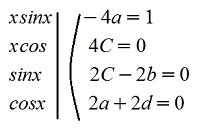
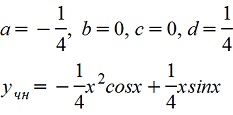
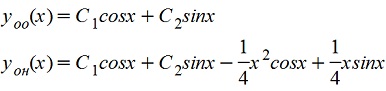
|  главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений обыкновенных дифференциальных уравнений порядка выше первого. / / Примеры решений линейных неоднородных уравнений с постоянными коэффициентами.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений обыкновенных дифференциальных уравнений порядка выше первого. / / Примеры решений линейных неоднородных уравнений с постоянными коэффициентами.
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений обыкновенных дифференциальных уравнений порядка выше первого. / / Примеры решений линейных неоднородных уравнений с постоянными коэффициентами.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Примеры решений обыкновенных дифференциальных уравнений порядка выше первого. / / Примеры решений линейных неоднородных уравнений с постоянными коэффициентами.
