Векторное произведение двух векторов. Он-лайн калькулятор.

Векторное произведение двух векторов. Он-лайн калькулятор.

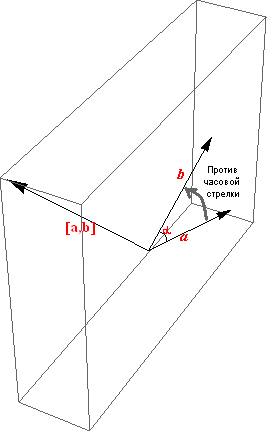
Векторное произведение двух векторов а и b - это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими свойствами: Для большей ясности приведем пример - на рисунке справа вектор [a,b] - векторное произведение векторов а и b. Как сказано в определении, мы привели все три вектора к общему началу, и тогда, если смотреть на вектора a и b с конца вектора [a,b], кратчайший поворот от вектора а до вектора b будет против часовой стрелки .

• Очевидно, что в случае векторного произведения, имеет значение порядок, в котором берутся вектора, более того,
  • 
• Так же, непосредственно из определения следует, что для любого скалярного множителя k (числа) верно следующее:
  • 
• Векторное произведение коллинеарных векторов равно нулевому вектору. Более того, векторное произведение двух векторов равно нулю тогда и только тогда, когда они коллинеарны. (В случае, если один из них нулевой вектор необходимо вспомнить, что нулевой вектор коллинеарен любому вектору по определению).
  • 
• Векторное произведение обладает распределительным свойством, то есть
  • 

Выражение векторного произведения через координаты векторов.

• Пусть даны два вектора
  • 
• (как найти координаты вектора по координатам его начала и конца - см. статью Скалярное произведение векторов, пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами.)
  • Тогда
  • 

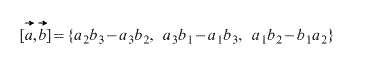
Зачем нужно векторное произведение?

Существует множество способов применения векторного произведения, например, как уже написано выше, вычислив векторное произведение двух векторов можно выяснить, коллинеарны ли они.

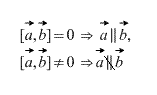
Или же его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина результирующего вектора и есть площадь данного параллелограмма.

Также огромное количество применений существует в электричестве и магнетизме.

Он-лайн калькулятор векторного произведения.

Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. статью Скалярное произведение векторов, пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )

Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. статью Скалярное произведение векторов, пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )