В механике существуют два типа величин:
- скалярные величины, задающие некоторое числовое значение - время, температура, масса и т.д.
- векторные величины, которые вместе с некоторым числовым значением задают направление - скорость, сила и т.д..
Рассмотрим сначала алгебраический подход к сложению векторов.
Покоординатное сложение векторов.
Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты - первую, из второй - вторую и т.д.):
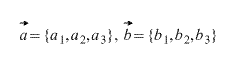
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
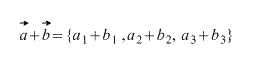
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов:
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
- правило параллелограмма
- правило треугольника
- тригонометрический способ
Правило параллелограмма. Сложение векторов по правилу параллелограмма. |
 |
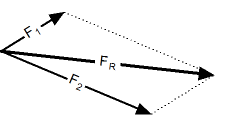Процедура сложения векторов по правилу параллелограмма заключается в следующем:
- нарисовать первый вектор, учитывая его величину и направление
- от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
- дополнить рисунок до параллелограмма, считая, что два нарисованных вектора - это его стороны
- результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.
|
Правило треугольника. Сложение векторов по правилу треугольника. |
 |
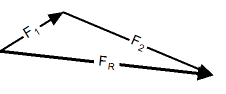Сложение векторов по правилу треугольника заключается в следующем:
- нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении
- от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление
- результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец - с концом второго.
|
Тригонометрический способ. Сложение векторов тригонометрическим способом. |
 |
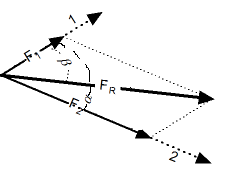Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
- Fрез. = [ F12 + F22 -2 F1 F2 cos(180о-α) ]1/2 (1)
- где
- F = числовое значение вектора
- α = угол между векторами 1 и 2
Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
- β = arcsin[ F2 *sin(180o-α) / FR ] (2)
- где
- α = угол между исходными векторами
|
Пример - сложение векторов.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Fрез = [ (5 кН)2 + (8 кН)2 - 2 (5 кН)(8 kН) cos(180o - (80o)) ]1/2
= 10,14кН
Угол между результирующей силой и первой силой равен:
β= arcsin[ (8кН) sin(180o - (80o)) / (10,14кН) ]
= 51o
А угол между второй и результирующей силой можно посчитать следующим образом: as
α = arcsin [ (5 кН) sin(180o - (80o)) / (10,2 кН) ]
= 29o
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
|
 |
главная страница / / Техническая информация / / Математический справочник / / Линейная алгебра. Вектора, матрицы, определители, миноры, детерминанты... / / Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.