Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.

Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.

Скалярное произведение векторов - это операция над двумя векторами, результатом которой является число (не вектор).

Определяется скалярное произведение, как правило, следующим образом:

Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними . Необходимо заметить, что угол между двумя векторами - это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать.

Непосредственно из определения следуют следующие простейшие свойства:

1. Скалярное произведение произвольного вектора а на себя же (скалярный квадрат вектора а) всегда неотрицательно, и равно квадрату длины этого вектора. Причем скалярный квадрат вектора равен нулю тогда и только тогда, когда данный вектор - нулевой.

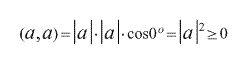
2.Скалярное произведение любых перпендикулярных векторов a и b равно нулю.

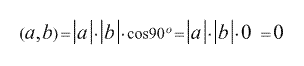
3. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перепендикулярны или хотя бы один из них - нулевой.

4. Скалярное произведение двух векторов a и b положительно тогда и только тогда, когда между ними острый угол.

5.Скалярное произведение двух векторов a и b отрицательно тогда и только тогда, когда между ними тупой угол.

Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами.

(Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто -

Пусть есть вектор AB, А - начало вектора, В - конец, и координаты этих точек

А=(a₁,a₂,a₃),        В=(b₁,b₂,b₃)

Тогда координаты вектора АВ:

АВ={b₁-a₁, b₂-a₂, b₃-a₃}.

Аналогично в двухмерном пространстве - просто отсутствуют третьи координаты)

Итак, пусть даны два вектора, заданные набором своих координат:

а) В двухмерном пространстве(на плоскости).

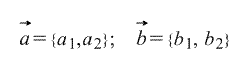
Тогда их скалярное произведение можно вычислить по формуле:

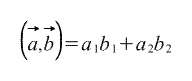
б) В трехмерном пространстве

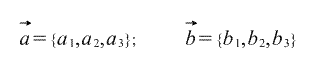
Аналогично двухмерному случаю, их скалярное произведение вычисляется по формуле:

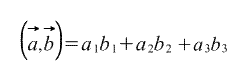
Вычисление угла между векторами с помощью скалярного произведения.

Самое распространенное математическое приложение скалярного произведения двух векторов - это вычисление угла между векторами, заданными своими координатами. Для примера возьмем трехмерный случай. (Если вектора заданы на плоскости, то есть двумя координатами, во всех формулах просто отсутствуют третьи координаты.)

Итак, пусть у нас есть два вектора:

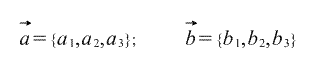
И нам нужно найти угол между ними. С помощью их координат найдем их длины, а затем просто приравняем две формулы для скалярного произведения. Таким образом мы получим косинус искомого угла.

Длина вектора а вычисляется как корень из скалярного квадрата вектора а, который мы вычислим по формуле для скалярного произведения векторов, заданных координатами:

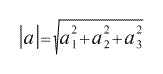
Аналогично вычисляется длина вектора b.

Итак,

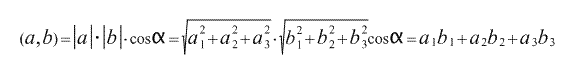
Значит,

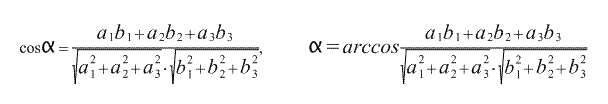
Искомый угол найден.

Он-лайн калькулятор скалярного произведения двух векторов.

Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. выше Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )

Если вектора заданы двумя координатами, то на месте третьей координаты каждого вектора нужно поставить ноль.

Он-лайн калькулятор угла между векторами.

Аналогично предыдущему калькулятору, необходимо ввести координаты обоих векторов по порядку, и если вектора заданы двумя координатами - на месте третьих координат следует поставить ноль.