Формулы объема
Объемы подобных тел.
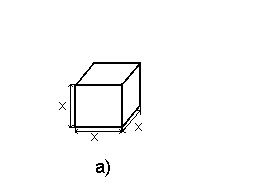
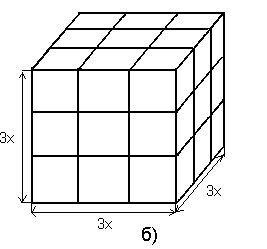
Объемы подобных тел пропорциональны кубам соответствующих линейных размеров.
Например, на рисунке выше показаны два куба, сторона одного из которых в 3 раза больше стороны другого.
Объем тела с рисунка а) V=x*x*x=x3
Объем тела с рисунка б) V=3x*3x*3x=27x3
Следовательно, тело на рис. б) имеет объем объем 33, т.е. его объем в 27 раз больше объема тела на рис. а).
Пример. Определение массы тела, подобного данному.
Масса автомобиля 1050 кг. Изготовлена модель автомобиля в масштабе 1:60. Определить массу модели автомобиля, если она слелана из того же материала, что и сам автомобиль.
Решение:
(Объем модели)/(объем автомобиля)=(1/60)3, поскольку объемы подобных тел пропорциональны кубам соостветствующих линейных размеров.
Масса =плотность*объем, а так как автомобиль и модель сделаны из одного материала, значит:
(Масса модели)/(Масса автомобиля)=(1/60)3
Следовательно,
Масса модели = (Масса автомашины) *(1/60)3=(10050)/(603)=0,0049 кг=4,9г.
Отношение объема к площади поверхности любого физического тела. Один из важнейших инженерных приемов.
 главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Объемы подобных тел.
главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Объемы подобных тел.
 главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Объемы подобных тел.
главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Объемы подобных тел.
