Формулы объема

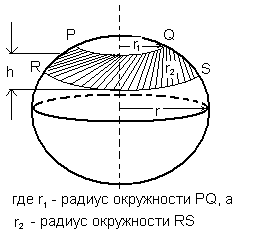
Объем шара равен 4/3π³ , а площадь сферы равна 4πr².

Шаровой слой - это часть шара между двумя параллельными плоскостями. На рисунке выше PQRS - шаровой слой.

Шаровой пояс - это сферическая поверхность шарового слоя.

Площадь шарового пояса на рисунке выше S=2 πhr;

Объем шарового слоя V=(πh/6)*(h²+3r₁²+3r₂²)

Пример1. Определение объема шарового слоя шара.

Определить объем шарового слоя шара с диаметром 50 см, если верхний и нижний диаметры слоя есть 25 и 40 см, а его высота 7,2 см.

Решение:

Как было сказано выше, объем шарового слоя

V=(πh/6)*(h²+3r₁²+3r₂²),

где h=7,2 см, r₁= 25/2=12,5 см, r₂=40/2=20 см

Следовательно, объем шарового слоя равен

V=(7,2π/6)*(7,2²+3*12,5²+3*20²)=6483,18 см² .

Пример 2. Определение площади шарового пояса.

Определить площадь шарового пояса из предыдущего примера.

Решение:

Площадь шарового пояса S=2πrh (как было определено выше), где радиус сферы r=50/2=25 см, а h=7,2 см.

Следовательно, площадь шарового пояса равна

S=2π*25*7,2=1130,4 см²

Пример 3. Определение объема заполнения сферического резервуара по уровню.

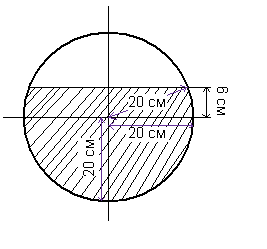
Сферический резервуар наполнен жидкостью до высоты 30 см. Определить объем жидкости в резервуаре (1л=1000 см³), если его внутренний диаметр равен 40 см.

Жидкость представлена в виде заштрихованной области в показанном на рис. ниже сечении.

Объем жидкости включает полусферу и шаровой пояс высотой 6 см.

Следовательно, объем жидкости есть V=(2/3)*πr³+(πh/6)*(h²+ 3r₁²+3r₂²), где

r₂=40/2=20 см и r₁=(20²-6²)^1/2=19,1 см

Объем жидкости V=2/3 π *20³+(6π)/6*(6²+3*19,1²+3*20²)=24064,22 см³

Поскольку 1 литр =1000 см³, то количество литров жидкости равно

24064,22/1000=24,06422 л.