Нахождение объемов неправильных тел с помощью формулы Симпсона.
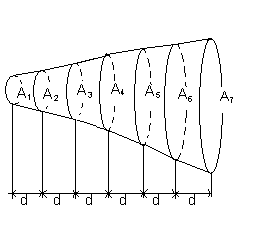
Если известны площади поперечных сечений А 1+А2+ А 3..., разделенные интервалом шириной d для неправильного тела, ограниченного двумя параллельными плоскостями (как показано на рис. выше), то объем по формуле Симпсона:
V=(d/3)*[(A1+A7) +4(A2+A4+ A 6)+2(A3+A5)]
Пример. Определение объема тела с переменным поперечным сечением.
Ствол дерева длиной 12 м имеет переменное поперечное сечение. Площади поперечных сечений, измеренные на расстоянии 2 м друг от друга, составляют 0,5; 0,57; 0,61; 0,65; 0,74; 0,86; 0,99 м2.
Оценим объем ствола дерева. Ствол дерева похож на набросок на рис. выше, где d=2 м, A1=0,5, A2=0,57, A3=0,61 и т.д.
Используя формулу Симпсона получаем,
V=(2/3)*[(0,5+0,99) +4(0,57+0,65+ 0,86 )+2(0,61+0,74)]=8,34 м3 |
главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Площади неправильных фигур, объемы неправильных тел. Средняя величина сигнала. Формулы и способы расчета площади. / / Нахождение объемов неправильных тел с помощью формулы Симпсона.