Однородные системы дифференциальных уравнений с постоянными коэффициентами. Теоретические сведения.
Рассматриваются системы дифференциальных уравнений вида
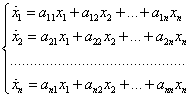
Здесь x
1(t), x
2(t), ... , x
n(t) - искомые функции, заданные на определенном промежутке (a, b), а a
ij (i, j=1, 2, ...n) - вещественные числа. Введем следующие обозначения:
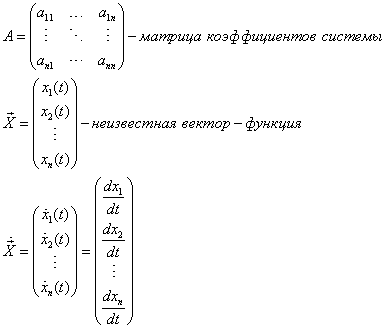
Используя операции над матрицами, исходную систему можно записать в следующем виде: 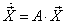
Прежде чем перейти непосредственно к решению таких систем, перечислим свойства решений этих систем.
Рассмотрим систему из n вектор-функций:
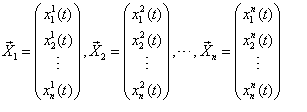
Определение 1.
Система вектор-функций 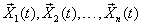 называется линейно зависимой на (a, b), если найдутся такие числа
называется линейно зависимой на (a, b), если найдутся такие числа 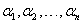 , не все равные нулю, что для любого t из промежутка (a, b)
, не все равные нулю, что для любого t из промежутка (a, b)
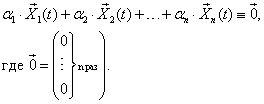
Если же тождество
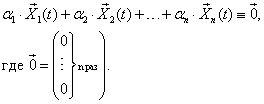
выполняется только при 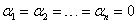 , то такая система вектор-функций
, то такая система вектор-функций 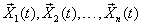 называется линейно независимой на интервале (a, b).
называется линейно независимой на интервале (a, b).
Определение 2.
Любая линейно независимая на (a, b) система n решений нашей системы дифференциальных уравнений называется фундаментальной системой решений.
Теорема 1.
Фундаментальная система решений существует. Вектор-функция
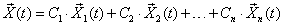 , где
, где 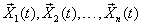 - фундаментальная система решений, C1, C2, ... , Cn - произвольные постоянные, является общим решением системы.
- фундаментальная система решений, C1, C2, ... , Cn - произвольные постоянные, является общим решением системы.
Определение 3.
Вектор 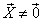 называется собственным вектором матрицы А, если найдется такое число
называется собственным вектором матрицы А, если найдется такое число 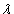 , что
, что
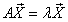 .
.
Тогда 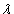 называется собственным значением матрицы А, соответствующим вектору X.
называется собственным значением матрицы А, соответствующим вектору X.
Для того, чтобы построить фундаментальную систему решений необходимо найти собственные значения матрицы А. Для их нахождения нужно решить так называемое характеристическое уравнение
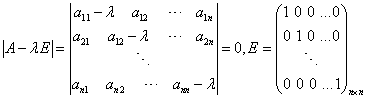 .
.
Данное уравнение является алгебраическим уравнением порядка n, следовательно, оно имеет n корней. Ход решение исходной системы зависит от структуры решения характеристического уравнения.
Для того, чтобы ознакомиться с алгоритмами решения однородных систем дифференциальных уравнений на примере систем третьего порядка, загляните сюда.
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Системы дифференциальных уравнений. Решение систем дифференциальных уравнений. / / Однородные системы дифференциальных уравнений. Решение. Теоретические сведения. / / Однородные системы дифференциальных уравнений с постоянными коэффициентами. Теоретические сведения.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Системы дифференциальных уравнений. Решение систем дифференциальных уравнений. / / Однородные системы дифференциальных уравнений. Решение. Теоретические сведения. / / Однородные системы дифференциальных уравнений с постоянными коэффициентами. Теоретические сведения.
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Системы дифференциальных уравнений. Решение систем дифференциальных уравнений. / / Однородные системы дифференциальных уравнений. Решение. Теоретические сведения. / / Однородные системы дифференциальных уравнений с постоянными коэффициентами. Теоретические сведения.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Системы дифференциальных уравнений. Решение систем дифференциальных уравнений. / / Однородные системы дифференциальных уравнений. Решение. Теоретические сведения. / / Однородные системы дифференциальных уравнений с постоянными коэффициентами. Теоретические сведения.
