Алгоритм решения линейных систем дифференциальных уравнений третьего порядка.
Для более глубокого понимания происходящего в этой статье можно ознакомиться с
краткой теоретической справкой.
Рассмотрим однородную систему дифференциальных уравнений третьего порядка
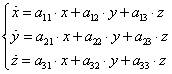
Здесь x(t), y(t), z(t) - искомые функции на промежутке (a, b), a
ij (i, j =1, 2, 3) - вещественные числа.
Запишем исходную систему в матричном виде
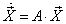
,
где

Решение исходной системы будем искать в виде
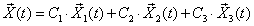
,
где
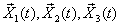
, C
1, C
2, C
3 - произвольные постоянные.
Чтобы найти фундаментальную систему решений, нужно решить так называемое характеристическое уравнение
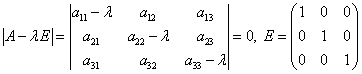
Это уравнение является алгебраическим уравнением третьего порядка, следовательно оно имеет 3 корня. При этом возможны следующие случаи:
1. Корни (собственные значения)
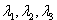
действительны и различны.
2. Среди корней (собственных значений) есть комплексно-сопряженные, пусть
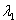
- действительный корень
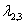
=
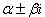
3. Корни (собственные значения) действительны. Один из корней кратный.
Чтобы разобраться, как действовать в каждом из этих случаев, нам понадобятся:
Теорема 1.
Пусть
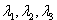
- попарно различные собственные значения матрица А, а
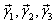
- соответствующие им собственные векторы. Тогда
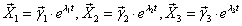
образуют фундаментальную систему решений исходной системы.
Замечание.
Пусть
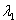
- действительное собственное значение матрица А (действительный корень характеристического уравнения),
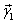
- соответствующий ему собственный вектор.
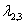
=
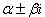
- комплексные собственные значения матрицы А,
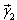
- соответствующий
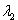
- собственный вектор. Тогда
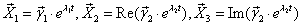
(Re - действительная часть, Im - мнимая)
образуют фундаментальную систему решений исходной системы. (Т.е.
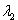
и
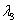
=
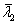
рассматриваются вместе)
Теорема 3.
Пусть - корень характеристического уравнения кратности 2. Тогда исходная система имеет 2 линейно независимых решения вида
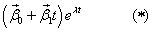
,
где
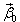
,
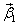
- постоянные вектора. Если же
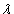
кратности 3, то существует 3 линейно независимых решения вида
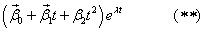
.
Векторы
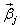
находятся подствалением решений (*) и (**) в исходную систему.
Чтобы лучше понять метод нахождения решений вида (*) и (**), смотри разобранные типичные примеры ниже.
Теперь рассмотрим более подробно каждый из вышеописанных случаев.
1. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае различных действительных корней характеристического уравнения.
Дана система
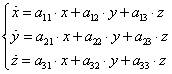
1) Составляем характеристическое уравнение
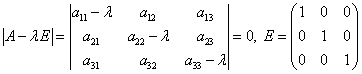
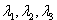
- действительные и различные собственные значения 9корни этого уравнения).
2)Строим
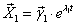
, где
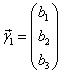
- собственный вектор матрицы А, соответствующий
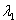
, т.е. - любое решение системы
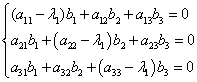
3)Строим
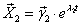
, где

- собственный вектор матрицы А, соответствующий
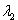
, т.е. - любое решение системы
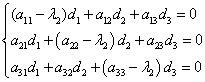
4)Строим
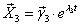
, где
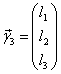
- собственный вектор матрицы А, соответствующий
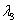
, т.е. - любое решение системы
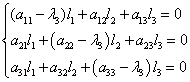
5)
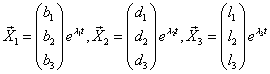
составляют фундаментальную систему решений. Далее записываем общее решение исходной системы в виде
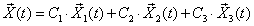
,
здесь C
1, C
2, C
3 - произвольные постоянные,
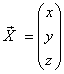
,
или в координатном виде
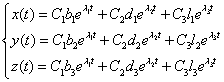
Расмотрим несколько примеров:
Пример 1.
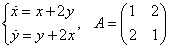
1)Составляем и решаем характеристическое уравнение:
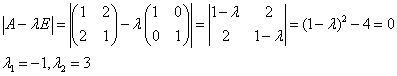
2) Находим

3)Находим

4)Вектор-функции
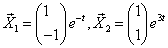
образуют фундаментальную систему. Общее решение имеет вид
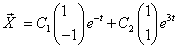
или в координатной записи
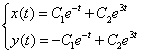 Пример 2.
Пример 2.
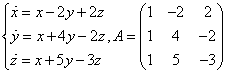
1)Составляем и решаем характеристическое уравнение:
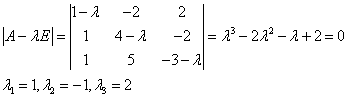
2) Находим
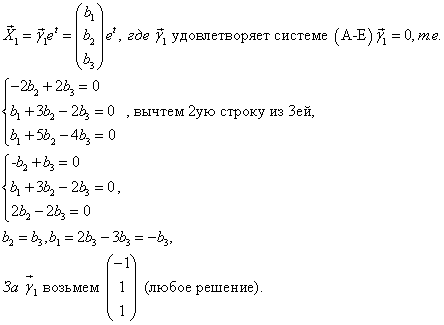
3)Находим
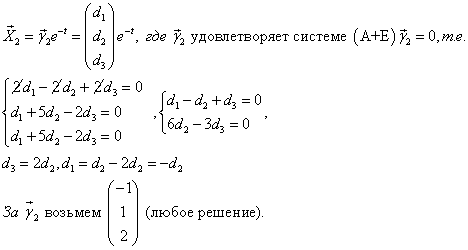
4)Находим
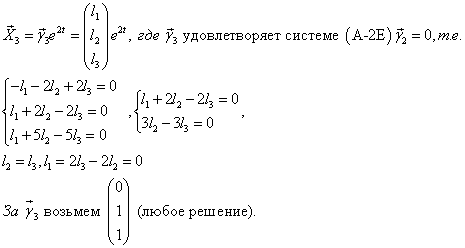
5)Вектор-функции
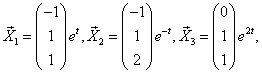
образуют фундаментальную систему. Общее решение имеет вид
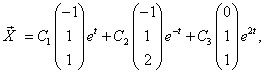
или в координатной записи
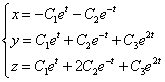 2. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае комплексно-сопряженных корней характеристического уравнения.
2. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае комплексно-сопряженных корней характеристического уравнения.
1) Составляем и решаем характеристическое уравнение
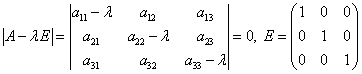
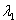
- действительный корень,
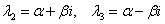
2)Строим
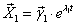
, где
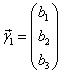 |
- собственный вектор матрицы А, соответствующий 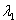 , т.е , т.е 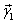 удовлетворяет системе удовлетворяет системе |
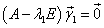 |
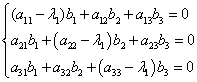
3) Строим
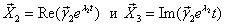
(т.е. 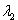 и
и 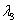 рассматриваем вместе), где
рассматриваем вместе), где
 |
- собственный вектор матрицы А, соответствующий 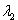 , т.е. , т.е. 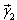 удовлетворяет системе удовлетворяет системе |
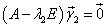 |
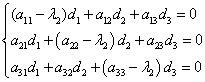
Здесь Re - действительная часть
Im - мнимая часть
4) 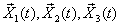 составляют фундаментальную систему решений. Далее записываем общее решение исходной системы:
составляют фундаментальную систему решений. Далее записываем общее решение исходной системы:
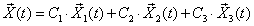 , где
, где
С1, С2,С3 произвольные постоянные.
Пример 1.
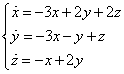
1) Составляем и решаем характеристическое уравнение
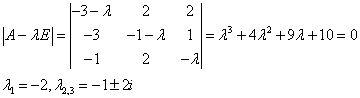
2)Строим
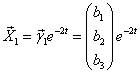 |
, где 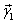 удовлетворяет системе удовлетворяет системе |
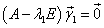 |
, т.е. |
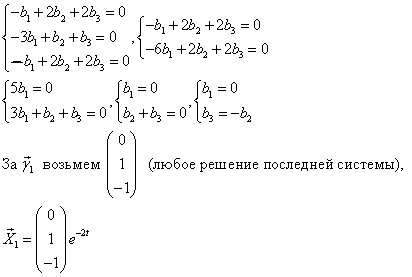
3) Строим
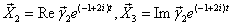 , где
, где
 |
- удовлетворяет системе |
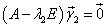 |
, т.е. |
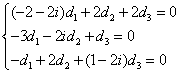
Первое уравнение сократим на 2. Затем ко второму уравнению прибавим первое, умноженное на 2i, а от третьего уравнения отнимем перове, умноженное на 2.
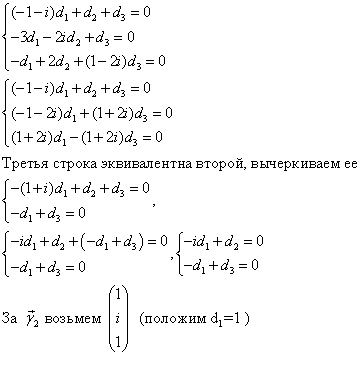
Далее
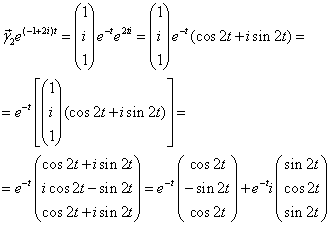
Следовательно,
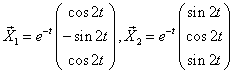
4) 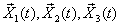 - фундаментальная система решений. Запишем общее решение исходной системы:
- фундаментальная система решений. Запишем общее решение исходной системы:
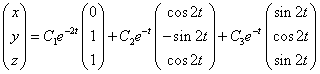
Пример 2.
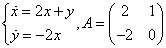
1) Составляем и решаем харктеристическое уравнение
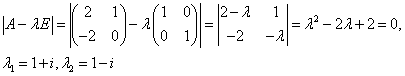
2)Строим
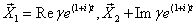
(т.е. 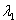 и
и 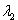 рассматриваем вместе), где
рассматриваем вместе), где
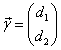 |
-собственный вектор матрицы А, соответствующий 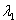 , т.е. любое решение системы , т.е. любое решение системы |
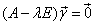 |
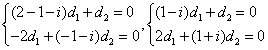
Второе уравнение умножим на (1-i) и сократим на 2.
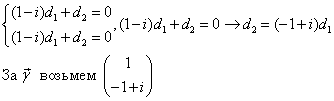
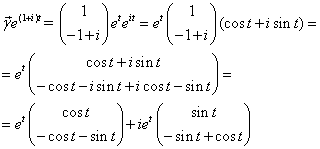
Следовательно,
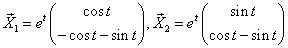
3) 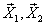 - фундаментальная система решений.
- фундаментальная система решений.
Общее решение исходной системы
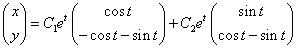
или
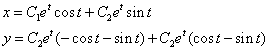
2. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае кратных корней характеристического уравнения.
Составляем и решаем характеристическое уравнение
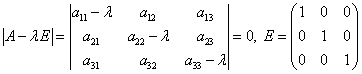
Возможны два случая:
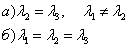
Рассмотрим случай а) 1) 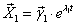 , где
, где
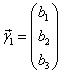 |
- собственный вектор матрицы А, соответствующий 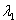 , т.е , т.е 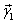 удовлетворяет системе удовлетворяет системе |
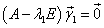 |
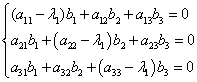
2) Сошлемся на Теорему 3, из которой следует, что существуют два линейно независимых решения вида
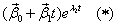 ,
,
где 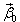 ,
, 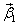 - постоянные векторы. Их возьмем за
- постоянные векторы. Их возьмем за 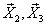 .
.
3)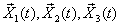 - фундаментальная система решений. Далее записываем общее решение исходной системы:
- фундаментальная система решений. Далее записываем общее решение исходной системы:
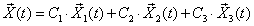
Рассмотрим случай б):
1) Сошлемся на Теорему 3, из которой следует, что существует три линейно независимых решения вида
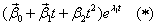 ,
,
где 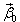 ,
, 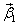 ,
, 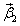 - постоянные векторы. Их возьмем за
- постоянные векторы. Их возьмем за 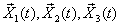 .
.
2)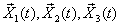 - фундаментальная система решений. Далее записываем общее решение исходной системы.
- фундаментальная система решений. Далее записываем общее решение исходной системы.
Чтобы лучше понять как находить решения вида (*), рассмотрим несколько типичных примеров.
Пример 1.
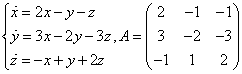
Составляем и решаем характеристическое уравнение:
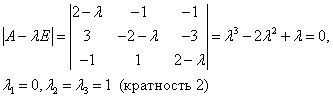
Имеем случай а)
1) Строим
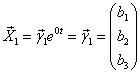 , где
, где
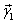 |
- любое решение системы |
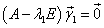 |
, т.е. |
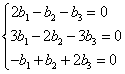
Из второго уравнения вычитаем первое:
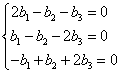 ? третья строка подобна второй, ее вычеркиваем. Из первого уравнения вычтем второе:
? третья строка подобна второй, ее вычеркиваем. Из первого уравнения вычтем второе:
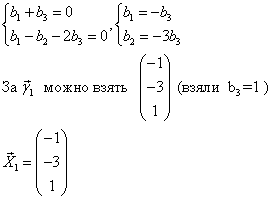
2) 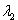 = 1 (кратность 2)
= 1 (кратность 2)
Этому корню по Т.3 должно соответствовать два линейно независимых решения вида 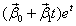 .
.
Попробуем найти все линейно незваисимые решения, у которых 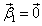 , т.е. решения вида
, т.е. решения вида
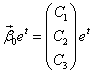 .
.
Такой вектор будет решением тогда и только тогда, когда 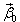 - собственный вектор, соответствующий
- собственный вектор, соответствующий 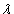 =1, т.е.
=1, т.е.
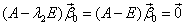 , или
, или
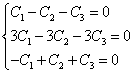 , вторая и третья строки подобны первой, выкидываем их.
, вторая и третья строки подобны первой, выкидываем их.
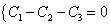
Система свелась к одному уравнению. Следовательно, имеется два свободных неизвестных, например, 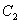 и
и 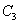 . Дадим им сначала значения 1, 0; потом значения 0, 1. Получим такие решения:
. Дадим им сначала значения 1, 0; потом значения 0, 1. Получим такие решения:
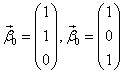 .
.
Следовательно, 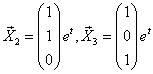 .
.
3) 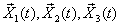 - фундаментальная система решений. Осталось записать общее решение исходной системы:
- фундаментальная система решений. Осталось записать общее решение исходной системы:
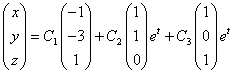 .
.
Пример 2.
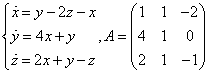
Составляем и решаем характеристическое уравнение:
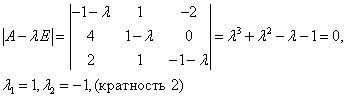
Имеем случай а).
1) Строим
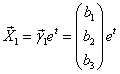 ,
,
| где |
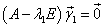 |
, т.е. |

За 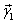 возьмем
возьмем
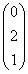 .Тогда
.Тогда
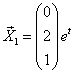
2) 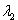 =-1 (кратности 2).
=-1 (кратности 2).
Этому корню по Т.3 соответствуют два линейно независимых решения вида 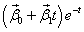 .
.
Попробуем найти линейно независимые решения, у которых 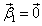 , т.е. решения вида
, т.е. решения вида 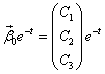
Но тогда 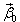 будет собственным вектором, соответствующим
будет собственным вектором, соответствующим 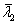 =-1, т.е.
=-1, т.е. 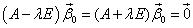 , т.е.
, т.е.
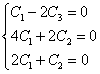
Третья строка аналогична второй, отбрасываем ее.
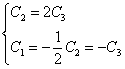
Пусть C3=1, тогда
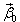 |
= |
 |
Итак, корню 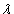 =-1 соответствует (в отличие от пример 1) один линейно независимый вектор
=-1 соответствует (в отличие от пример 1) один линейно независимый вектор 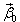 . Любой другой собственный вектор имеет вид
. Любой другой собственный вектор имеет вид 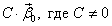 . Таким образом существует только одно решение вида
. Таким образом существует только одно решение вида 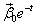 . Следовательно,
. Следовательно,
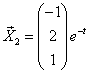 .
.
Следующий вектор фундаментальной системы решений будем искать в виде
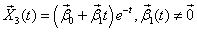
Чтобы понять, как искать 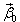 и
и 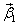 в этом случае, воспользуемся матричной записью системы:
в этом случае, воспользуемся матричной записью системы:
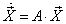
Подставим X3 в эту систему:
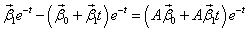
Сократим на e-t и приравняем коэффициенты при одинаковых степенях t. Получаем систему
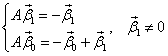
Из первого уравнения и условия 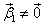 следует, что
следует, что 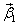 - собственный вектор, отвечающий собственнуму значению
- собственный вектор, отвечающий собственнуму значению 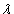 , т.е.
, т.е.
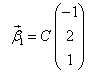
| [ |
 |
нашли, когда искали |
Х2] |
Второе уравнение последней системы запишем так:
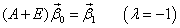
Этому матричному уравнению соответствует система линейных уравнений:
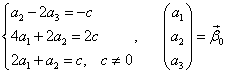
Вычеркнем третью строку (она подобна второй). Система совместна (имеет решение) при любом с. Пусть с=1.
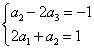
Выпишем какое-нибудь частное решение последней системы.
a3=0, a2=-1, a1=1 т.е.
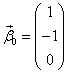
Тогда
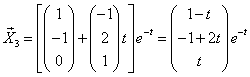
3) 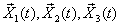 - фундаментальная система решений. Выпишем общее решение исходной системы:
- фундаментальная система решений. Выпишем общее решение исходной системы:
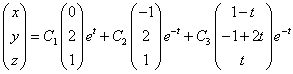
или
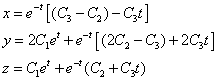
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Системы дифференциальных уравнений. Решение систем дифференциальных уравнений. / / Однородные системы дифференциальных уравнений. Решение. Теоретические сведения. / / Алгоритм решения линейных систем дифференциальных уравнений третьего порядка.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Системы дифференциальных уравнений. Решение систем дифференциальных уравнений. / / Однородные системы дифференциальных уравнений. Решение. Теоретические сведения. / / Алгоритм решения линейных систем дифференциальных уравнений третьего порядка.
 главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Системы дифференциальных уравнений. Решение систем дифференциальных уравнений. / / Однородные системы дифференциальных уравнений. Решение. Теоретические сведения. / / Алгоритм решения линейных систем дифференциальных уравнений третьего порядка.
главная страница / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений. / / Системы дифференциальных уравнений. Решение систем дифференциальных уравнений. / / Однородные системы дифференциальных уравнений. Решение. Теоретические сведения. / / Алгоритм решения линейных систем дифференциальных уравнений третьего порядка.
