Численное решение уравнений. Вводные замечания. Итерационные методы. Признак сходимости и оценка ошибки. Правило ложного положения (метод секущих). Улучшение сходимости по Эйткену-Стеффенсену. Вычисление значений многочлена. Последовательные умножения. Схема Горнера. Общие методы.
Меню:
Вводные замечания.
Численному решению уравнения f(z)=0 должно быть предпослано хотя бы грубое исследование вопросов существования и положения корней, их оценка и т.д. Решения могут быть проверены подстановкой.
Итерационные методы.
Данное уравнение
f(z)=0 приводят к виду z=φ(z).
Выбирая некоторое начальное приближение z[o], вычисляют последовательные приближения
z[j+1]=φ(z[j]) (j=0,1,2..).
Сходимость таких приближений к искомому решению z требует отдельного исследования. Итерации заканчивают тогда, когда отношение
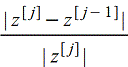 , становится достаточно малым. , становится достаточно малым.
Признак сходимости и оценка ошибки.
Если существует такая область D в комплексной плоскости и такое положительное число M<1, что
|φ(Z1)-φ(Z2)|≤M|Z1-Z2| для всех Z1,Z2 из D, и если D содержит z[o], z[1] и все точки z удовлетворяют неравенству
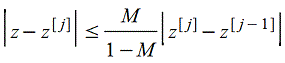
для каждого значения j ≥1, то приближения z[j+1]=φ(z[j]) сходятся к некоторому решению z уравнения f(z)=0; это решение удовлетворяет неравенству
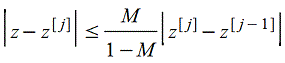
и является единственным в D. Заметим, что правая часть данного неравенства дает верхнюю грань ошибки j-го приближения z[j].
Возможны различные способы приведения уравнения f(z)=0к виду z=φ(z). Вот некоторые итерационные формулы, основанные на специальном выборе функции φ(z).
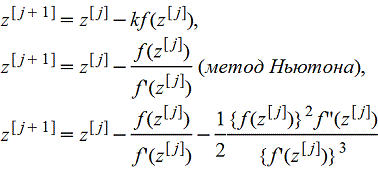
Эти итерационные формулы особенно удобны при вычислении действительных корней. Для нахождения комплексных корней действительных уравнений надо выбирать комплексное начальное приближение z[o]. Признак сходимости и оценка ошибки применимы во всех случаях. Метод Ньютона есть частный случай общего метода Ньютона.
Общий метод Ньютона.
Если производная f'(z) непрерывно дифференцируема в рассматриваемой области и если можно найти такие положительные числа A, B, C что
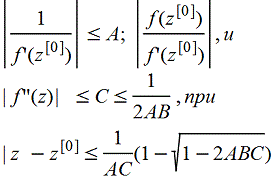 , ,
то искомый корень z удовлетворяет последнему неравенству и быстрота сходимости метода Ньютона оценивается неравенством
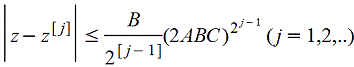
Отметим, что здесь имеет место относительно быстрая сходимость.
Правило ложного положения (метод секущих).
Правило ложного положения отличается от приведенных выше итерационных методов тем, что для определения нового приближения z[j+1] используют два предыдущих. Для решения уравнения f(z)=0 выбирают два начальных приближения z[o], z[1] и строят последовательные приближения
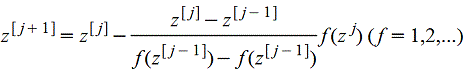 . .
Для отыскания действительных корней действительных уравнений приближение z[j+1] обычно строят по z[j] и z[k], где k=k(j)<j - наибольший индекс, такой, что f(z[k]) и f(z[j]) имеют разные знаки:
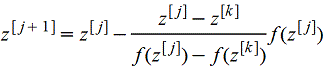 . .
В часности, разные знаки должны иметь f(z[o]) и f(z[1]); при указанной схеме обеспечена локализация корня z[k] и z[j].
Улучшение сходимости по Эйткену-Стеффенсену.
Если φ(z) действительна и трижды непрерывно дифференцируема в окресности действительного корня z, причем φ'(z)≠1, то сходимость итерационного процесса z[j+1]=φ(z[j]) можно улучшить с помощью следующей итерационной схемы:
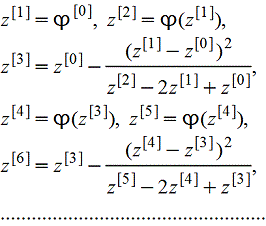 (формула 1) (формула 1)
Итерации заканчивают, когда один из знаменателей оказывается близким к нулю. Этот метод, подобно методу секущих, может применяться вместо быстро сходящегося метода Ньютона, если вычисление значений f'(z) вызывает затруднения.
Вычисление значений многочлена .
Последовательные умножения.
Для применения рассматриваемых далее итерационных методов надо уметь вычислять значения многочлена
f(z)≡ aozn+ a1zn-1+ ...+ an-1z+ an
Для этой цели либо вычисляют последовательно aoz+a1z(aoz+a1)+a2, ..., либо предварительно находят величины f(c), f'(c), 1/2f''(c), ... по схеме Горнера и затем пользуются формулой 1.
Схема Горнера.
Деление многочлена f(z) на (z-c) дает новый многочлен f1(z) и остаток f(с); деление f1(z) на (z-c) дает многочлен f2(z) и остаток f'(z). Продолжая этот процесс, получаем последовательно остатки f(c), f'(c), 1/21f''(c), 1/31f'''(c), ..., которые являются коэффициентами разложения многочлена F(u)≡ f(u+c)≡f(c)+f'(c)u+(1/21)*f''(c)u2+... (1/n!)*f(n)(c)un≡f(z)
Схема Горнера для комплексного аргумента.
Если f(z) - многочлен с действительными коэффициентами, а c=a+ib, то f(c)=Ac+B=(Aa+B)+iAb, где Az+B - действительный остаток от деления f(z) на (z2-2az+a2+b2).
Итерационные методы.
Общие методы (метод Мюллера, метод Бэрстоу).
Чтобы вычислить изолированный простой корень алгебраического уравнения
f(z)≡ aozn+ a1zn-1+ ...+ an-1z+ an =0 ,
можно:
1) применить метод Ньютона
2) применить метод секущих
3) воспользоваться методом Горнера
Метод Мюллера.
Вместо линейной интерполяции метода секущих здесь применяется квадратичная интерполяция, что приводит к итерации вида
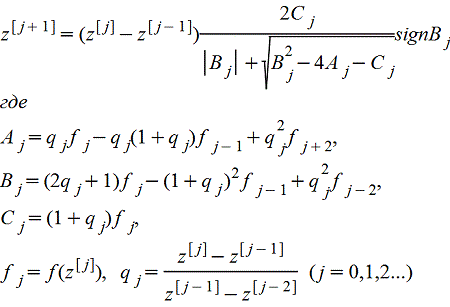
Для начала решения можно положить
z[o]=-1, z[1]=1, z[2]=0, (q2=1/2)
и
fo=an-an-1+an-2+..., f1=an+an-1+an-2+..., f2=an
Метод Мюллера распространяется также и на неалгебраические уравнения.
Метод Бэрстоу.
Пусть многочлен f(z)≡aozn+a1zn-1+...+an-1z+an содержит квадратный множитель z2-uz-v, определяющий два различных простых корня уравнения f(z)≡ aozn+ a1zn-1+ ...+ an-1z+ an =0 , и пусть известны достаточно хорошие начальные приближения u[o] и v[o] для u и v. Тогда последовательность лучших приближений, сходящихся к u и v, дается формулами
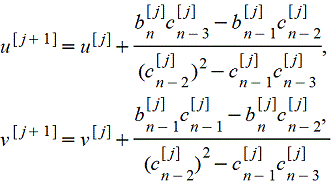
где величины b[j]k, c[j]k вычисляются последовательно для каждого j по формулам
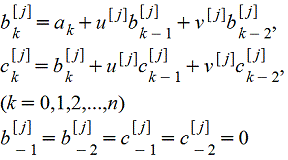
|
 главная страница / / Техническая информация / / Математический справочник / / Численные методы / / Численное решение уравнений. Вводные замечания. Итерационные методы. Признак сходимости и оценка ошибки. Правило ложного положения (метод секущих). Улучшение сходимости по Эйткену-Стеффенсену. Вычисление значений многочлена.
главная страница / / Техническая информация / / Математический справочник / / Численные методы / / Численное решение уравнений. Вводные замечания. Итерационные методы. Признак сходимости и оценка ошибки. Правило ложного положения (метод секущих). Улучшение сходимости по Эйткену-Стеффенсену. Вычисление значений многочлена.
 главная страница / / Техническая информация / / Математический справочник / / Численные методы / / Численное решение уравнений. Вводные замечания. Итерационные методы. Признак сходимости и оценка ошибки. Правило ложного положения (метод секущих). Улучшение сходимости по Эйткену-Стеффенсену. Вычисление значений многочлена.
главная страница / / Техническая информация / / Математический справочник / / Численные методы / / Численное решение уравнений. Вводные замечания. Итерационные методы. Признак сходимости и оценка ошибки. Правило ложного положения (метод секущих). Улучшение сходимости по Эйткену-Стеффенсену. Вычисление значений многочлена.
