Численное решение уравнений. Метод Греффе-Лобачевского. Метод Горнера. Итерационные методы. Метод наискорейшего спуска. Метод Ньютона и теорема Канторовича.
Меню:
Вводные замечания.
Численному решению уравнения f(z)=0 должно быть предпослано хотя бы грубое исследование вопросов существования и положения корней, их оценка и т.д. Решения могут быть проверены подстановкой.
Метод Греффе-Лобачевского.
Если дано алгебраическое уравнение с действительными коэффициентами
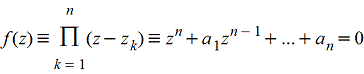
то сначала находят коэффициенты aji многочлена
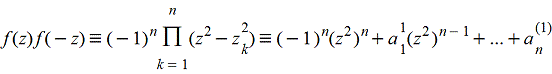
с помощью таблицы
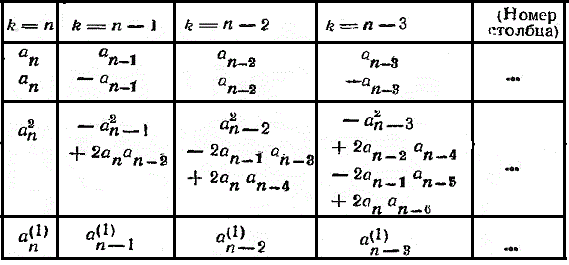
Повторяя этот процесс, получают последовательно коэффициенты aji, многочленов
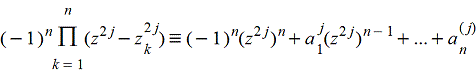
При возрастании j столбцы в расчетных таблицах оказываются одного из трех типов:
1) В некоторых столбцах удвоенные произведения становятся пренебрежимо малыми, так что последовательные записи в этих столбцах становятся квадратами с одинаковыми знаками (правильные столбцы); если последовательные записи имеют одинаковые знаки, а их абсолютные значения оказываются равными определенной доле квадрата предыдущего значения, то мы имеем частично правильные столбцы.
2) Записи столбцов могут иметь чередующиеся знаки (колеблющиеся столбцы).
3) Некоторые столбцы могут не обладать указанной выше правильностью.
Каждая пара правильных столбцов (например, k и k-r), разделенная r-1 неправильными столбцами, соответствует r корням z с равными модулями.
Эти r корней все либо действительны, либо чисто мнимы, если r-1 разделяющих столбцов частично правильны.
Метод Горнера.
Метод Горнера (для действительных корней) сводится к последовательному вычислению коэффициентов многочленов
F1(u)≡f(u+c1), F2(u)≡F1(u+c2), ... по схеме Горнера, где c1, c2 выбираются так, чтобы уменьшить абсолютные величины остатков. Если удается получить Fj(0)≈0, то искомый корень приближенно равен c1+c2+...+cj;
Итерационные методы.
Задача решения системы n уравнений
f1=fi(x1, x2, ..., xn)=0 (i=1, 2, ..., n) с неизвестными x1, x2, ..., xn эквивалентна задаче минимизации функции
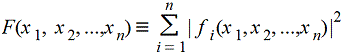 , ,
или какой-либо другой возрастающей функции от абсолютных величин |fi| - невязок (ошибок) f1=fi(x1, x2, ..., xn)=0, (i=1, 2, ..., n). Задача отыскания минимума (максимума ) функции n переменных и сама по себе имеет большое практическое значение.
Для решения этой задачи итерационными методами начинают с произвольных значений xi[o] (i=1,2,...,n) и строят последовательные приближения xi[j+1]=xi[j]+λjvi[j] (i=1,2,...,n; j=0,1,2,...), которые сходятся к некоторому решению xi при j→∞.
Различные методы отличаются выбором "направления" j-го шага, т.е. выбором отношений v1j : v2j : ... : vnj. Величина шага определяется значением параметра λj, минимизирующим величину F(x1[j+1],x2[j+1],..., xn[j+1]) как функцию от λj. Последний метод применим для отыскания max и min таблично заданной функции F(x1,x2,..., xn). На каждом шаге изменяют только одно из xi , либо циклически, либо так, чтобы уменьшить наибольшую по модулю невязку.
Методы поиска.
Чисто случайный поиск состоит в отборе наибольшего (наименьшего) из значений F(x1,x2,..., xn) для некоторого количества случайно выбранных точек (x1,x2,..., xn), он применяется, главным образом, при отыскании начальных приближений для итерационных методов. В методе случайных возмущений начинают с некоторой точки (x1,x2,..., xn) и вводят множество случайных возмущений всех неизвестных Δx1,Δx2,...,Δxn для получения большего (меньшего) значения исследуемой функции F. Рассчитанная при этом точка дает следующее приближение, и поиск продолжается. При этом методе, в отличие от метода чисто случайного поиска, можно использовать свойство непрерывности исследуемой функции. Метод случайных возмущений часто применяется в тех случаях, когда градиентые методы отказывают из-за таких особенностей многомерной области, как "хребты", "ущелья", "плоскогорья" и кратные экстремумы. Дальнейшее развитие этого метода приводит к стратегиям, включающим изменение шага и предпочтение определенных направлений, зависящих от прошлых успехов или промахов.
Метод наискорейшего спуска.
Выбирают vi[j]=-δF/δxi , где все производные вычисляются при xi=xij, и уменьшают величину шага λ[j] по мере приближения к минимуму функции F. Для аналитических функций F и малых значений fi тейлоровское разложение F(λ[j]) позволяет выбрать оптимальную величину шага
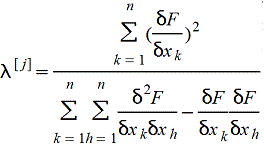 . .
где все производные вычисляются при xi=xi[j]. Параболическая интерполяция функции F(λ[j]) может оказаться более удобной.
Спуск с вычислением координат градиента.
Часто вычисление координат вектора градиента δF/δxk , необходимых для метода наискорейшего спуска, оказывается невозможным или непрактичным. Тогда указанные производные заменяют разностными отношениями ΔF/Δxk, получаемыми путем поочередного изменения только одного переменного xk . Так как при этом на каждый шаг расчета в направлении градиента затрачивается n шагов расчета координат градиента, то предпочитают продолжать расчеты в вычмсленном направлении до тех пор, пока больше нельзя уточнить исследуемую функцию, и только после этого снова пересчитывать координаты градиента.
Метод Ньютона и теорема Канторовича.
Метод Ньютона.
Выбирая некоторое начальное приближение xi[o], находят последовательные приближения xi[j+1] путем решения системы линейных уравнений
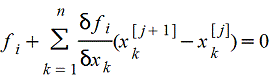 , (i=1,2,...,n) , (i=1,2,...,n)
где значения функции fi n частных производных δfi/δxk ерутся при xk=xk[j], j=0,1,2,...
Теорема Канторовича о сходимости .
Предположим, что матрица [δfi/δxk] имеет обратную матрицу [δfi/δxk]-1≡ [Гik(x1, x2,...,xn]-1для рассматриваемых значений xk.
Пусть A, B, C - такие положительные числа, что в начальной точке xi=xi[o]
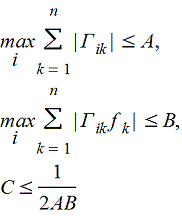
Если fi(x1,x2,...,xn) дважды непрерывно дифференцируемы и удовлетворяют условию
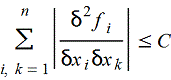
для всех точек (x1,x2,...,xn)в кубической области
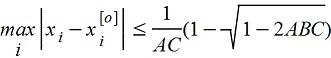
то система fi(x1,x2,...,xn)=0 имеет решение (x1,x2,...,xn) в той же кубической области и скорость сходимости оценивается так:
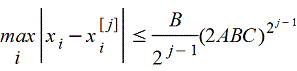
Это указывает на относительно быструю сходимость.
|
 главная страница / / Техническая информация / / Математический справочник / / Численные методы / / Численное решение уравнений. Метод Греффе-Лобачевского. Метод Горнера. Итерационные методы. Метод наискорейшего спуска. Метод Ньютона и теорема Канторовича.
главная страница / / Техническая информация / / Математический справочник / / Численные методы / / Численное решение уравнений. Метод Греффе-Лобачевского. Метод Горнера. Итерационные методы. Метод наискорейшего спуска. Метод Ньютона и теорема Канторовича.
 главная страница / / Техническая информация / / Математический справочник / / Численные методы / / Численное решение уравнений. Метод Греффе-Лобачевского. Метод Горнера. Итерационные методы. Метод наискорейшего спуска. Метод Ньютона и теорема Канторовича.
главная страница / / Техническая информация / / Математический справочник / / Численные методы / / Численное решение уравнений. Метод Греффе-Лобачевского. Метод Горнера. Итерационные методы. Метод наискорейшего спуска. Метод Ньютона и теорема Канторовича.
