Примеры некоторых распространенных разложений периодических и непереодических функций в ряд Фурье на интервале 2π.
1) Функция
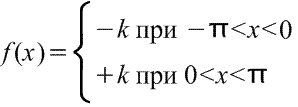 (Функция является периодической за пределами заданного диапазона с интервалом 2π) (Функция является периодической за пределами заданного диапазона с интервалом 2π)
Этот прямоугольный сигнал показан на рис. ниже. Поскольку f(x) для двух половин диапазона задается двумя различными выражениями, интегрирование сигнала проводим для двух интервалов - сначала от -π до 0, затем от 0 до π.
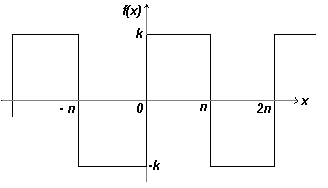
Отсюда коэффициенты Фурье:
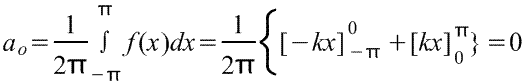
(В действительности ao - это среднее значение функции за полный период 2π, и его равенство 0 очевидно из рис. )
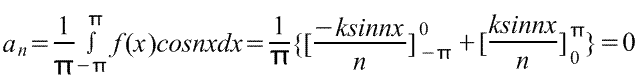
Следовательно, a1, a2, a3, ... все равны 0 (поскольку sin0=sin(-nπ)=sinnπ=0), и поэтому в ряду Фурье нет членов с косинусами.
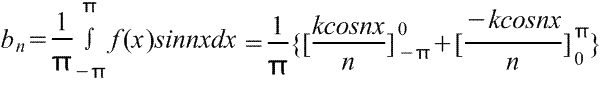
Если n - нечетное,
bn=4k/nπ,
Следовательно, b1=4k/π, b3=4k/3π, b5=4k/5π и так далее,
Если n четное bn=0.
Следовательно, согласно основной формуле разложения в ряд Фурье для функции на рис. выше есть
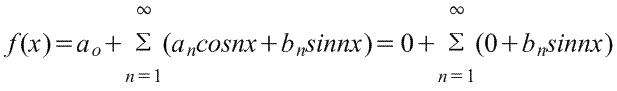
т.е.
Ответ1:
f(x)=(4k/π)sinx+(4k/3π)sin3x+(4k/5π)sin5x+...
Ответ2:
f(x)=4k/π(sinx+1/3πsin3x+1/5sin5x+...)
Если в рассмотренном выше ряду Фурье k=π, то f(x)=4[(sinx+(1/3)sin3x+(1/5π)sin5x+...]. Выражение 4sinx называется первой частичной суммой ряда Фурье функции f(x), (4sinx+(4/3)sin3x) - второй частичной суммной ряда Фурье, (4sinx+(4/3)sin3x+(4/5π)sin5x) - третьей частичной суммой ряда Фурье и так далее.
Пусть Р1=4sinx, Р2=(4sinx+(4/3)sin3x) , Р3=(4sinx+(4/3)sin3x+(4/5π)sin5x)
Графики Р1, Р2, Р3 построены по таблицам значений, а их суммы показаны на трех рис. ниже, откуда видно, что ряд сходится, т.е.при увеличении количества рассматриваемых частичных сумм он стремиться к конечному пределу, и в пределе получается сумма f(x)= π. Даже при учете только трех частичных сумм форма графика приближается к прямоугольной, которую представляет ряд Фурье.
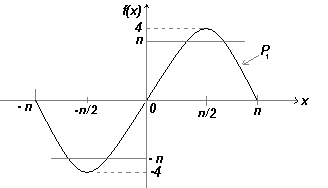
1) Первая частичная сумма ряда Фурье функции f(x) |
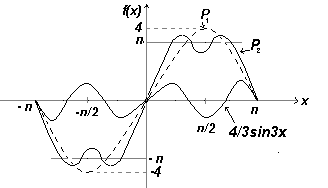
2) Вторая частичная сумма ряда Фурье функции f(x) |
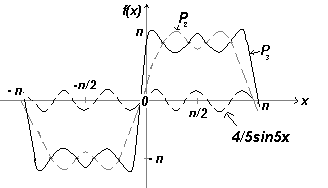
3) Третья частичная сумма ряда Фурье функции f(x) |
2) Функция f(x)=2xна диапазоне от - π до π
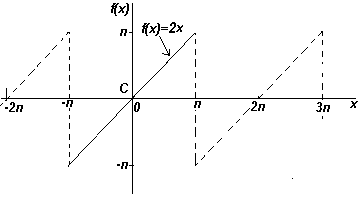
Для данного уравнения:
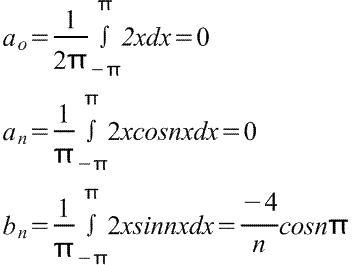
Ответ:
2х= 4[(sinx-(1/2)sin2x+(1/3)sin3x-1/4sin4x+1/5sin5x-1/6sin6x+...) |
3) Функция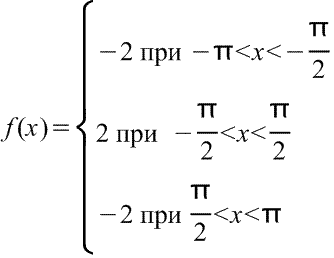 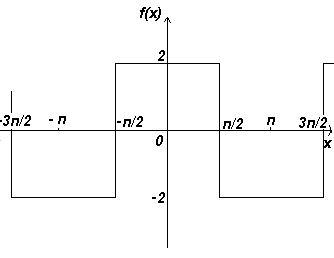
Для данного уравнения :
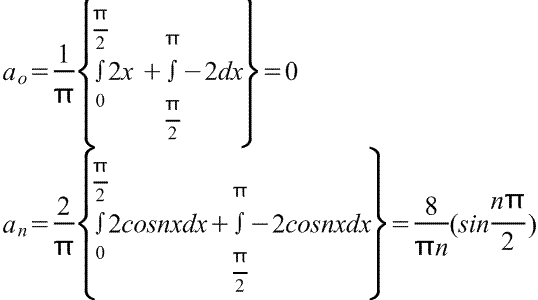
Ответ:
f(x)=8/π(cosx-1/3cos3x+1/5cos5x-1/7cos7x+...) |
4) Функция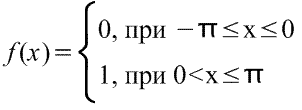 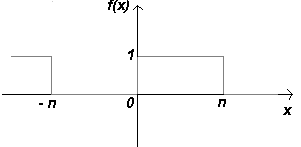
Коэффициенты:
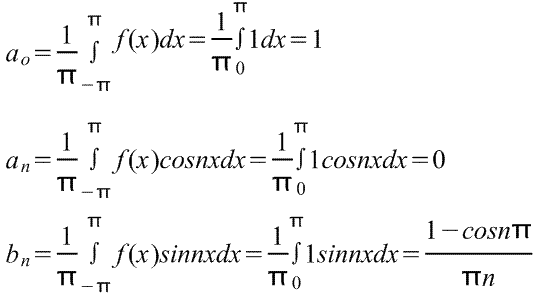
Ответ:
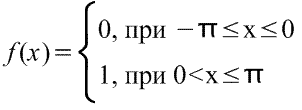
|
5) Функция f(x)=x2
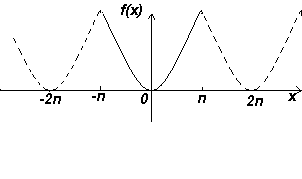
Коэффициенты:
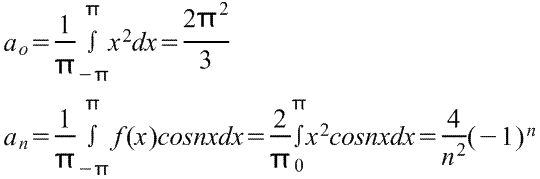
Ответ:
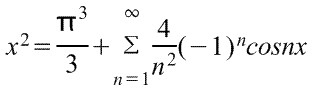
|
6) Функция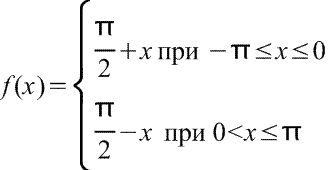
Коэффициенты:
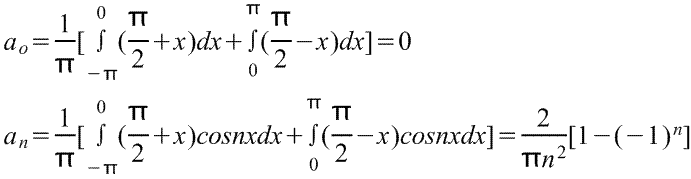
Ответ:
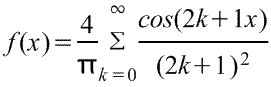
|
7) Функция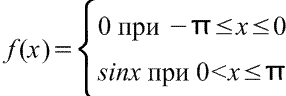
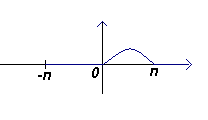
Коэффициенты:
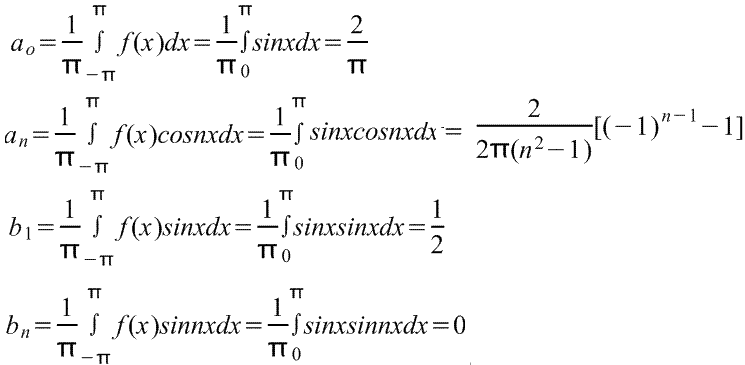
Ответ:
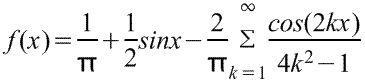
|
|
 главная страница / / Техническая информация / / Математический справочник / / Степенные ряды Тейлора, Маклорена (=Макларена) и периодический ряд Фурье. Разложение функций в ряды. / / Примеры некоторых распространенных разложений периодических и непереодических функций в ряд Фурье на интервале 2π.
главная страница / / Техническая информация / / Математический справочник / / Степенные ряды Тейлора, Маклорена (=Макларена) и периодический ряд Фурье. Разложение функций в ряды. / / Примеры некоторых распространенных разложений периодических и непереодических функций в ряд Фурье на интервале 2π.
 главная страница / / Техническая информация / / Математический справочник / / Степенные ряды Тейлора, Маклорена (=Макларена) и периодический ряд Фурье. Разложение функций в ряды. / / Примеры некоторых распространенных разложений периодических и непереодических функций в ряд Фурье на интервале 2π.
главная страница / / Техническая информация / / Математический справочник / / Степенные ряды Тейлора, Маклорена (=Макларена) и периодический ряд Фурье. Разложение функций в ряды. / / Примеры некоторых распространенных разложений периодических и непереодических функций в ряд Фурье на интервале 2π.
