Практические задачи с использованием тригонометрии.
Существует ряд практических ситуаций, в которых необходимо использовать тригонометрию для определения неизвестных сторон и углов треугольников.
- Пример 1
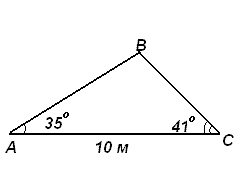
- Здание шириной 10 м имеет двускатную крышу с наклоном 35o с одной стороны и 41o - с другой. Найти длину скатов крыши с точностью до сантиметра.
- Пример 2
- На рис. показаны два вектора напряжения, V1=50В и V2=90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V1
- Пример 3
- На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью и длину ОВ в положении, показанном на рис.
- Пример 4
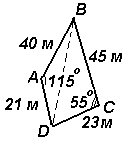
- Поле имеет форму четырехугольника ABCD, показанного на рис. ниже. Определить площадь поля.
Пример 1 Здание шириной 10 м имеет двускатную крышу с наклоном 35o с одной стороны и 41o - с другой. Найти длину скатов крыши с точностью до сантиметра.
Решение:
Угол конька крыши В=180o - 35o- 41o=104o
По теореме синусов
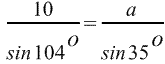 , ,
Откуда
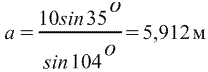 . .
Также по теореме синусов:
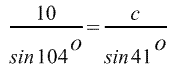
Откуда
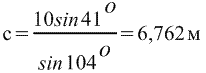 . .
(используется таблица синусов)
Следовательно, длины скатов крыши равны 6 м и 7 м с точностью до см.
Примечание: сторона а - сторона против угла А, сторона с - сторона против угла С.
Пример 2 На рис. показаны два вектора напряжения, V1=50В и V2=90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V1.
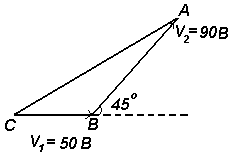
Решение:
<CAB=180o - 45o=135o.
Согласно теореме косинусов:
СА2 = V12+V22 - 2V1V2 cosCBA=
=502 + 902 - 2*50*90cos135o=16963.(по таблице косинусов)
Результирующий вектор CA=(16963)1/2 =130,2B.
Cогласно теореме синусов,
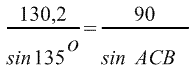 , ,
Откуда
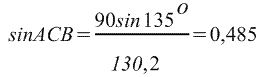 , ,
Следовательно угол АСВ приблизительно равен 29о. (по таблице синусов)
Итак, результирующий вектор напряжения равен 130,2В и составляет угол в 29о с V1
Пример 3 На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью и длину ОВ в положении, показанном на рис.
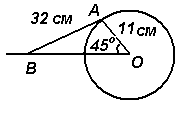
Решение:
По теореме синусов,
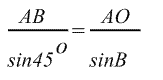 , откуда , откуда
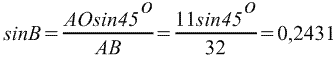
Значит, В=arcsin0,2431≈ 14 o (по таблице синусов )
Следовательно, шатун AB составляет угол 14 o с горизонталью.
<ОАВ=180o-45o-14o=121o
По теореме синусов:
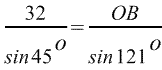 , откуда , откуда
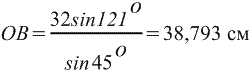
Пример 4 Поле имеет форму четырехугольника ABCD, показанного на рис. Определить площадь поля.
Проведенная из В в D диагональ делит четырехугольник на два треугольника.
Решение:
Площадь четырехугольника ABCD= площадь треугольника ABD+площадь треугольника BCD, т.е.
SABCD =1/2*(40)*(21)*sin115o + 1/2*(45)*(23)*sin55o=804,582 м2
|
 главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg....Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Практические задачи с использованием тригонометрии.
главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg....Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Практические задачи с использованием тригонометрии.
 главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg....Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Практические задачи с использованием тригонометрии.
главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg....Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Практические задачи с использованием тригонометрии.
