Геометрическая прогрессия.
Геометрическая прогрессия — последовательность чисел b1, b2, b3,.. (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q (знаменатель прогрессии), где b1≠0 , q≠0.
- b1, b2=b1q, b3=b2q, ..., bn=bn-1q...
- где q знаменатель геометрической прогрессии (шаг),
- b1, b2, b3, ..., bn,.. - члены геометрической прогрессии
- n-й член геометрической прогрессии bn определяется по формуле:
- Если b1 > 0 и q > 1, прогрессия является возрастающей последовательностью,
- если 0 < q < 1, — убывающей последовательностью,
- а при q < 0 — знакопеременной.
Формулы суммы первых n членов геометрической прогрессии:
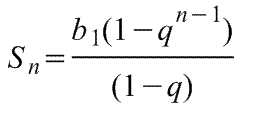 , что верно при q < 1 , что верно при q < 1
или
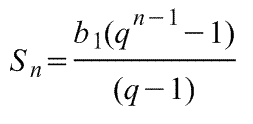 ,что верно при q > 1 ,что верно при q > 1
Сумма бесконечной геометрической прогрессии:
Если знаменатель геометрической прогрессии q < 1, то сумму первых n членов геометрической прогрессии (см. выше) можно записать как
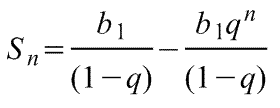 . .
Поскольку q < 1, при увеличении n, q уменьшится.
.gif) . .
Величина [b1/(1-q) ] называется суммой бесконечной геометрической прогрессии S∞, она ограничивает значение суммы бесконечного количества членов прогрессии, т.е.
Формула суммы бесконечной геометрической прогрессии имеет вид
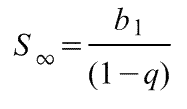
- , что верно при -1 < q < 1
- Говорят, что бесконечная геометрическая прогрессия сходится, если предел lim Snпри n→∞ существует и конечен.
- В противном случае прогрессия расходится.
|
 главная страница / / Техническая информация / / Математический справочник / / Арифметическая, Геометрическая прогрессии и суммы некоторых числовых рядов. / / Геометрическая прогрессия.
главная страница / / Техническая информация / / Математический справочник / / Арифметическая, Геометрическая прогрессии и суммы некоторых числовых рядов. / / Геометрическая прогрессия.
 главная страница / / Техническая информация / / Математический справочник / / Арифметическая, Геометрическая прогрессии и суммы некоторых числовых рядов. / / Геометрическая прогрессия.
главная страница / / Техническая информация / / Математический справочник / / Арифметическая, Геометрическая прогрессии и суммы некоторых числовых рядов. / / Геометрическая прогрессия.
